Vector Control: Bed nets

# Load the requisite packages:
library(malariasimulation)
# Set colour palette:
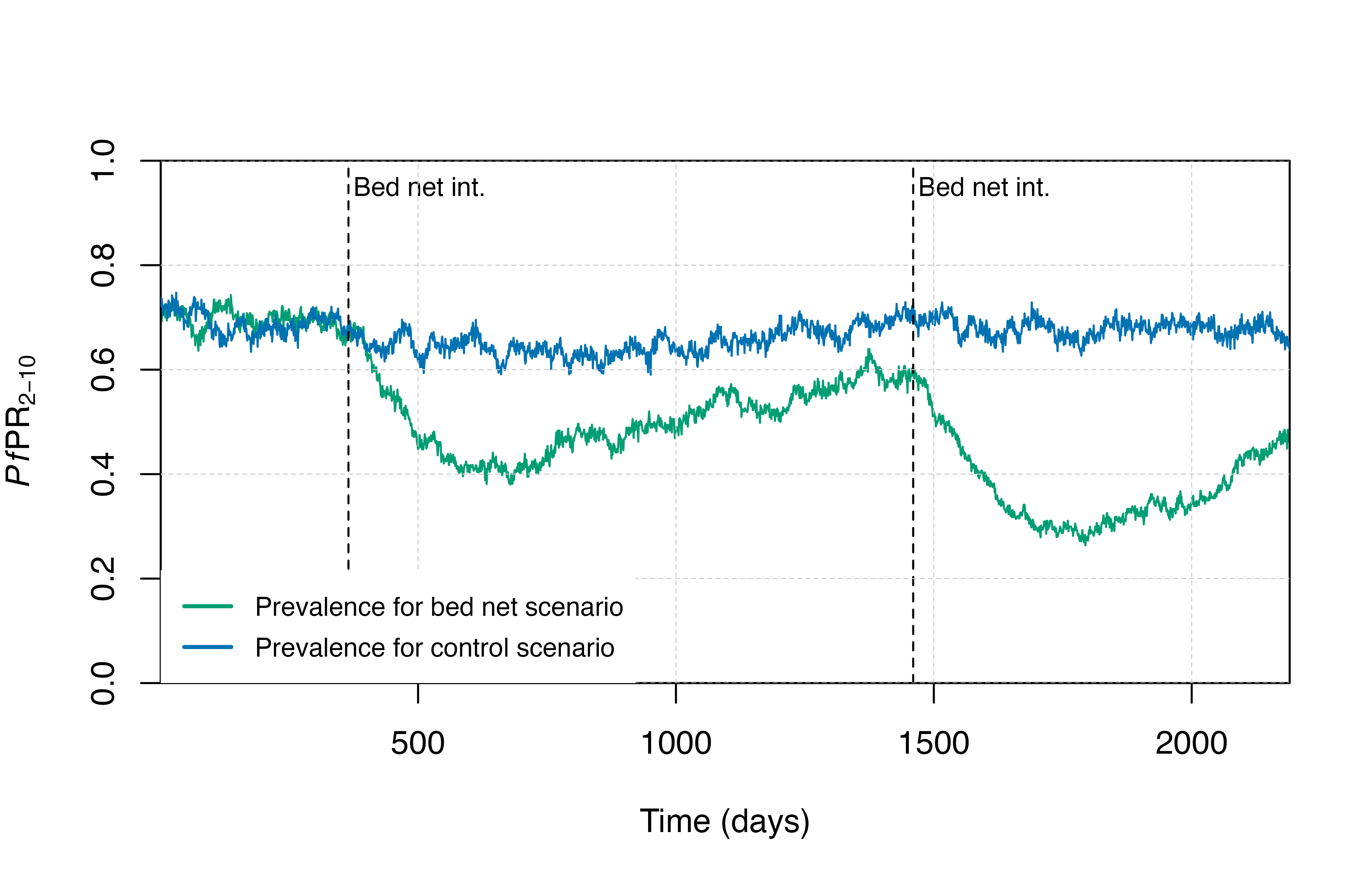
cols <- c("#E69F00", "#56B4E9", "#009E73", "#F0E442", "#0072B2", "#D55E00", "#CC79A7")

Long-lasting insecticide-treated bed nets are a highly effective intervention to prevent malaria. The effects of insecticide-treated bed net distribution campaigns can be simulated using malariasimulation. The model provides the user with the flexibility to specify parameters that describe the net distribution campaign (e.g. timing, coverage, and target population) and the bed nets distributed (e.g. efficacy, longevity). We will illustrate this through an example with two bed net distributions, once per year.

We can create a few plotting functions to visualise the output.

# Plotting functions
plot_prev <- function() {
  plot(x = output$timestep, y = output$n_detect_lm_730_3650 / output$n_age_730_3650, 
       type = "l", col = cols[3], lwd = 1,
       xlab = "Time (days)", ylab = expression(paste(italic(Pf),"PR"[2-10])),
       xaxs = "i", yaxs = "i", ylim = c(0, 1))
  lines(x = output_control$timestep, y = output_control$n_detect_lm_730_3650 / output_control$n_age_730_3650,
        col = cols[5], lwd = 1)
  abline(v = bednetstimesteps, col = "black", lty = 2, lwd = 1)
  text(x = bednetstimesteps + 10, y = 0.95, labels = "Bed net int.", adj = 0, cex = 0.8)
  grid(lty = 2, col = "grey80", lwd = 0.5)
  legend("bottomleft", box.lty = 0, bg = "white",
         legend = c("Prevalence for bed net scenario","Prevalence for control scenario"),
         col = c(cols[3], cols[5]), lty = c(1,1), lwd = 2, cex = 0.8, y.intersp = 1.3)
}

Setting bed net parameters

Parameterisation

Use the get_parameters() function to generate the list of parameters for a perennial profile, accepting the default values to run the simulation from an equilibrium starting point.

year <- 365
sim_length <- 6 * year
human_population <- 1000
starting_EIR <- 50

simparams <- get_parameters(
  list(human_population = human_population)
)

simparams <- set_equilibrium(parameters = simparams, init_EIR = starting_EIR)

output_control <- run_simulation(timesteps = sim_length, parameters = simparams)

A note on mosquito species

It is also possible to use the set_species() function to account for 3 different mosquito species in the simulation. In this case, the matrices would need to have additional column corresponding to each mosquito species. For example, if we specified that there were 3 species of mosquitoes in the model and nets were distributed at two timesteps, then the matrices would have 2 rows and 3 columns. If you are not already familiar with the set_species() function, see the Mosquito Species vignette.

The default parameters are set to model Anopheles gambiae.

simparams$species
#> [1] "gamb"
simparams$species_proportions
#> [1] 1

Simulation

Having established a base set of parameters, we can now create a copy of this parameter list and update it to specify a net distribution campaign. In the example below, we distribute bed nets to a random 50% of the population every three years. It is possible to change the characteristics of the bed nets for each distribution timestep if different types of bed nets are distributed that have different insecticides, different levels of insecticide resistance, etc. This can be done by modifying the matrices for dn0, rn, rnm, and gamman. Because we are using the default proportions of mosquito species and there are two timesteps when nets are distributed, the matrices for dn0, rn, and rnm have 1 column and 2 rows.

The parameter values for pyrethroid-only and pyrethroid-PBO nets at various resistance levels can be found in Table S1.3 in the Supplementary Appendix 2 of Sherrard-Smith, et al., 2022.

bednetstimesteps <- c(1, 4) * year # The bed nets will be distributed at the end of the first and the 4th year. 

bednetparams <- set_bednets(
  simparams,
  timesteps = bednetstimesteps,
  coverages = c(.5, .5),  # Each round is distributed to 50% of the population.
  retention = 5 * year, # Nets are kept on average 5 years
  dn0 = matrix(c(.533, .533), nrow = 2, ncol = 1), # Matrix of death probabilities for each mosquito species over time
  rn = matrix(c(.56, .56), nrow = 2, ncol = 1), # Matrix of repelling probabilities for each mosquito species over time
  rnm = matrix(c(.24, .24), nrow = 2, ncol = 1), # Matrix of minimum repelling probabilities for each mosquito species over time
  gamman = rep(2.64 * 365, 2) # Vector of bed net half-lives for each distribution timestep
)

output <- run_simulation(timesteps = sim_length, parameters = bednetparams)

Visualisation

# Plot prevalence
plot_prev()

Comparing coverage and population bed net usage

It is important to understand the difference between the input coverages argument of set_bednets() and the resulting population bed net usage over time in the model. When we set coverages in the above example to 0.5, we are telling the model to distribute bed nets to a random 50% of the population at year one and to a random 50% of the population at year 4. However, the level of average bed net usage is not necessarily equal to 50%. Between these time points, bed net use will slowly decline over time (in reality this decline stems from things like disuse, holes in nets, lost nets, etc.).

The average population bed net usage will be influenced by:

• The size and frequency of distributions specified in set_bednets()
  
• The assumed net retention half life (gamman)
• Correlations in the recipients of nets between rounds

The output from malariasimulation::run_simulation() has a variable n_use_net that shows the number of people using bed nets at any given timestep. We can visualise the proportion of the population using bed nets over time to understand how bed net usage changes.

output$prop_use_net <- output$n_use_net / human_population

plot(x = output$timestep, y = output$prop_use_net, type = "l", 
     col = cols[3], lwd = 2.5, ylim = c(0,1),
     xlab = "Timestep (days)", ylab = "Proportion of population using bed nets",
     xaxs = "i", yaxs = "i")
grid(lty = 2, col = "grey80", lwd = 0.5)
axis(side = 1, lty = 1, col = "black", pos = 0); axis(side = 2, lty = 1, col = "black")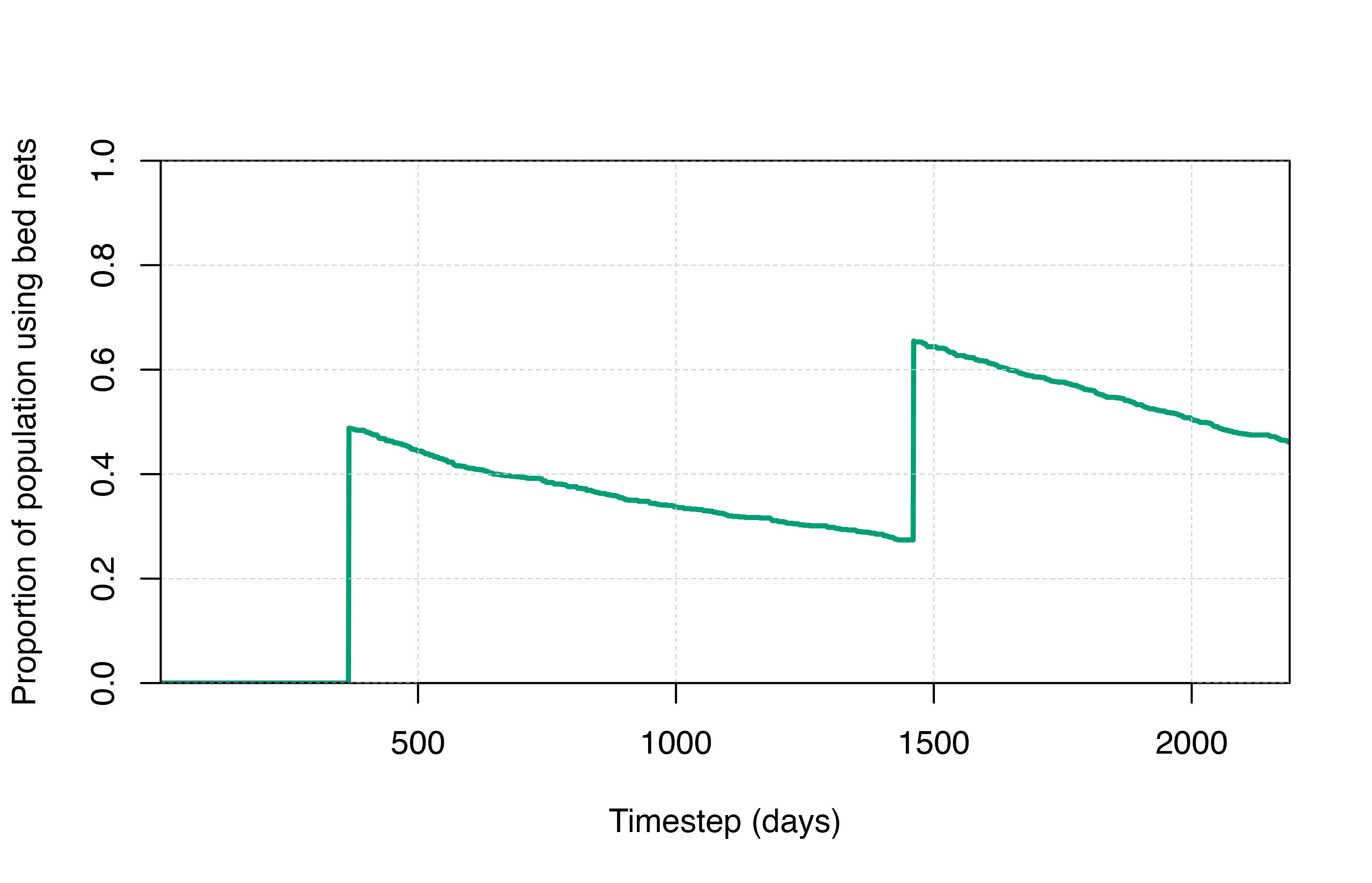

Using the netz package

The netz package is a useful tool to help set up bed nets in malariasimulation. malariasimulation takes as an input the proportion of the population who were distributed a bed net at specific time points, but net distribution or use data are now always available for a specific region or country. netz has functionality to estimate modelled population usage over time in the simulation for a given set of input distributions. It can also help to fit the input coverages to usage data.

See this vignette from the netz package that demonstrates how to estimate population bed net usage from an input distribution.