Skip to contents

Getting started with odin2

Source: vignettes/odin2.Rmd
odin2.Rmd

odin2 implements a high-level language for describing and implementing ordinary differential equations and difference equations in R. It provides a “domain specific language” (DSL) which looks like R but is compiled directly to C++, using dust2 to solve your system and to provide an interface to particle filters. You can then use monty to fit your models using MCMC.

This vignette jumps through a few of the core features of odin2 and ways that you might use it with dust2 and monty. The other vignettes and the odin & monty book expand on topics covered here in more detail.

Discrete time stochastic SIR model

A simple definition of the SIR model is:

dSdt=−βSINdIdt=βSIN−γIdRdt=γI\begin{align*} \frac{dS}{dt} &= -\beta \frac{SI}{N} \\ \frac{dI}{dt} &= \beta \frac{SI}{N} - \gamma I \\ \frac{dR}{dt} &= \gamma I \\ \end{align*}

where SS is the number of susceptibles, II is the number of infected and RR is the number recovered; the total population size N=S+I+RN = S + I + R is constant. β\beta is the infection rate, γ\gamma is the recovery rate.

Discretising this model in time steps of width dtdt gives the following update equations for each time step:

St+1=St−nSIIt+1=It+nSI−nIRRt+1=Rt+nIR\begin{align*} S_{t+1} &= S_t - n_{SI} \\ I_{t+1} &= I_t + n_{SI} - n_{IR} \\ R_{t+1} &= R_t + n_{IR} \end{align*}

where

nSI∼Binomial(S,1−e−βIN⋅dt)nIR∼Binomial(I,1−e−γ⋅dt)\begin{align*} n_{SI} &\sim \mathrm{Binomial}(S, 1 - e^{-\beta \frac{I}{N} \cdot dt}) \\ n_{IR} &\sim \mathrm{Binomial}(I, 1 - e^{-\gamma \cdot dt}) \end{align*}

Here is this system, as a stochastic compartmental model:

gen <- odin2::odin({
  p_IR <- 1 - exp(-gamma * dt)
  N <- parameter(1000)

  p_SI <- 1 - exp(-(beta * I / N * dt))
  n_SI <- Binomial(S, p_SI)
  n_IR <- Binomial(I, p_IR)

  update(S) <- S - n_SI
  update(I) <- I + n_SI - n_IR
  update(R) <- R + n_IR

  initial(S) <- N - I0
  initial(I) <- I0
  initial(R) <- 0

  beta <- parameter(0.2)
  gamma <- parameter(0.1)
  I0 <- parameter(10)
})
#> ✔ Wrote 'DESCRIPTION'
#> ✔ Wrote 'NAMESPACE'
#> ✔ Wrote 'R/dust.R'
#> ✔ Wrote 'src/dust.cpp'
#> ✔ Wrote 'src/Makevars'
#> ℹ 12 functions decorated with [[cpp11::register]]
#> ✔ generated file cpp11.R
#> ✔ generated file cpp11.cpp
#> ℹ Re-compiling odin.system3c679b6a
#> ── R CMD INSTALL ───────────────────────────────────────────────────────────────
#> * installing *source* package ‘odin.system3c679b6a’ ...
#> ** this is package ‘odin.system3c679b6a’ version ‘0.0.1’
#> ** using staged installation
#> ** libs
#> using C++ compiler: ‘g++ (Ubuntu 13.3.0-6ubuntu2~24.04) 13.3.0’
#> g++ -std=gnu++17 -I"/opt/R/4.5.1/lib/R/include" -DNDEBUG  -I'/home/runner/work/_temp/Library/cpp11/include' -I'/home/runner/work/_temp/Library/dust2/include' -I'/home/runner/work/_temp/Library/monty/include' -I/usr/local/include   -DHAVE_INLINE -fopenmp  -fpic  -g -O2  -Wall -pedantic -fdiagnostics-color=always  -c cpp11.cpp -o cpp11.o
#> g++ -std=gnu++17 -I"/opt/R/4.5.1/lib/R/include" -DNDEBUG  -I'/home/runner/work/_temp/Library/cpp11/include' -I'/home/runner/work/_temp/Library/dust2/include' -I'/home/runner/work/_temp/Library/monty/include' -I/usr/local/include   -DHAVE_INLINE -fopenmp  -fpic  -g -O2  -Wall -pedantic -fdiagnostics-color=always  -c dust.cpp -o dust.o
#> g++ -std=gnu++17 -shared -L/opt/R/4.5.1/lib/R/lib -L/usr/local/lib -o odin.system3c679b6a.so cpp11.o dust.o -fopenmp -L/opt/R/4.5.1/lib/R/lib -lR
#> installing to /tmp/Rtmp7IUxzh/devtools_install_21536cc142ea/00LOCK-dust_2153122e8f43/00new/odin.system3c679b6a/libs
#> ** checking absolute paths in shared objects and dynamic libraries
#> * DONE (odin.system3c679b6a)
#> ℹ Loading odin.system3c679b6a

This step generates C++ code for the model and compiles it; it will take a few seconds.

Once we have our system, we can pass it to [dust2::dust_system_create] to create and start simulating it. Our system above has defaults for its parameters (N, beta, gamma, and I0) so we can initialise with almost no arguments:

pars <- list(beta = 0.2, gamma = 0.1, I0 = 10, N = 1000)
sys <- dust2::dust_system_create(gen(), pars, n_particles = 10)

By default the system will start at time 0 and with dt = 1. We can simulate 10 random epidemics starting from our initial conditions:

dust2::dust_system_set_state_initial(sys)
time <- 0:100
y <- dust2::dust_system_simulate(sys, time)
matplot(time, t(y[2, , ]), col = "#00000055", lty = 1, type = "l",
        xlab = "Time", ylab = "Number of infecteds")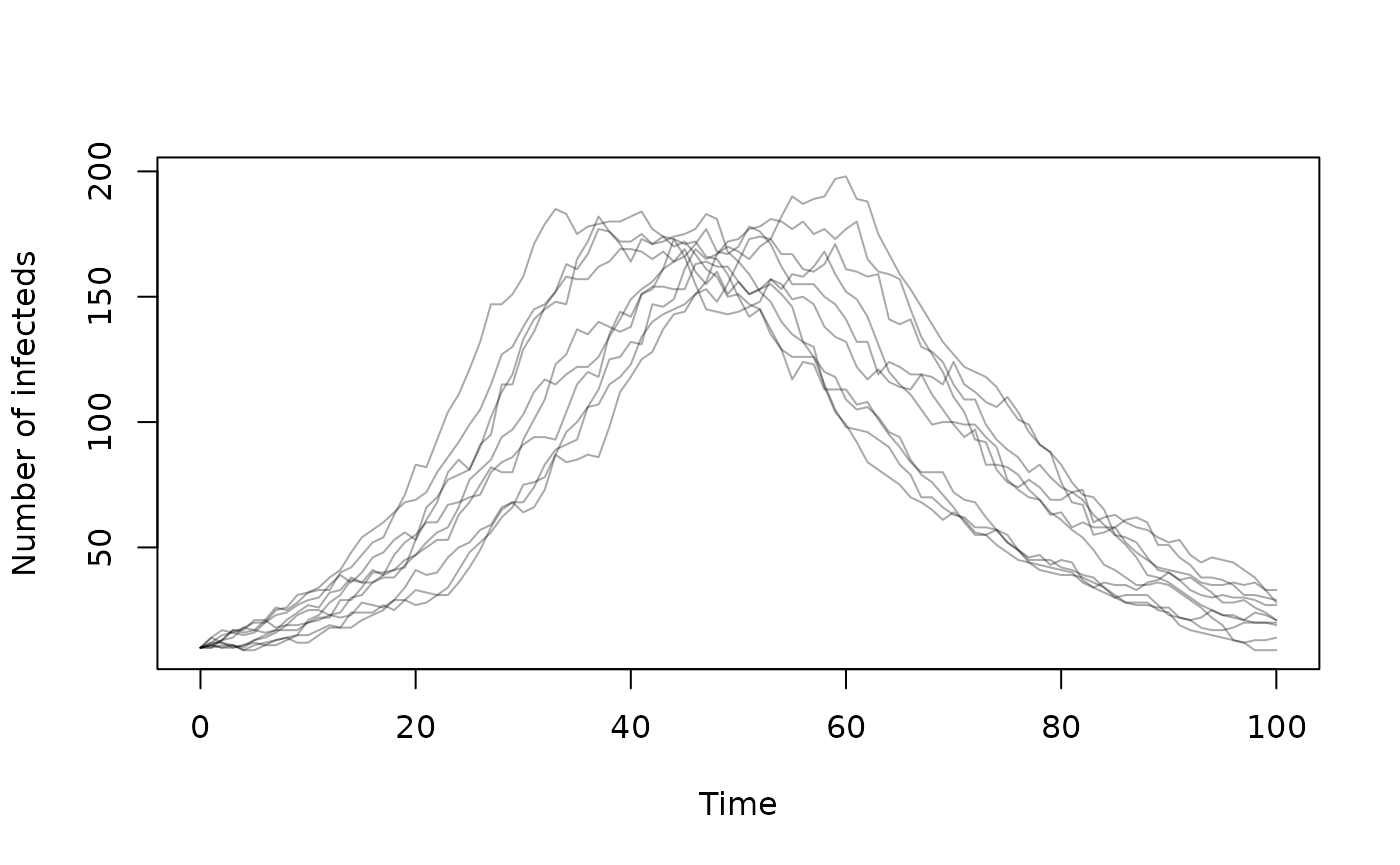

as this system is stochastic, each trajectory will be different.