Discretized Generation Time Distribution Assuming A Shifted Gamma Distribution

discr_si computes the discrete distribution of the serial interval, assuming that the serial interval is shifted Gamma distributed, with shift 1.

discr_si(k, mu, sigma)

Arguments

k: Positive integer, or vector of positive integers for which the discrete distribution is desired.
mu: A positive real giving the mean of the Gamma distribution.
sigma: A non-negative real giving the standard deviation of the Gamma distribution.

Value

Gives the discrete probability $w_k$ that the serial interval is equal to $k$.

Details

Assuming that the serial interval is shifted Gamma distributed with mean $\mu$, standard deviation $\sigma$ and shift $1$, the discrete probability $w_k$ that the serial interval is equal to $k$ is:$$w_k = kF_{\{\mu-1,\sigma\}}(k)+(k-2)F_{\{\mu-1,\sigma\}} (k-2)-2(k-1)F_{\{\mu-1,\sigma\}}(k-1)\\ +(\mu-1)(2F_{\{\mu-1+\frac{\sigma^2}{\mu-1}, \sigma\sqrt{1+\frac{\sigma^2}{\mu-1}}\}}(k-1)- F_{\{\mu-1+\frac{\sigma^2}{\mu-1}, \sigma\sqrt{1+\frac{\sigma^2}{\mu-1}}\}}(k-2)- F_{\{\mu-1+\frac{\sigma^2}{\mu-1}, \sigma\sqrt{1+\frac{\sigma^2}{\mu-1}}\}}(k))$$where $F_{\{\mu,\sigma\}}$ is the cumulative density function of a Gamma distribution with mean $\mu$ and standard deviation $\sigma$.

References

Cori, A. et al. A new framework and software to estimate time-varying reproduction numbers during epidemics (AJE 2013).

Author

Anne Cori a.cori@imperial.ac.uk

Examples

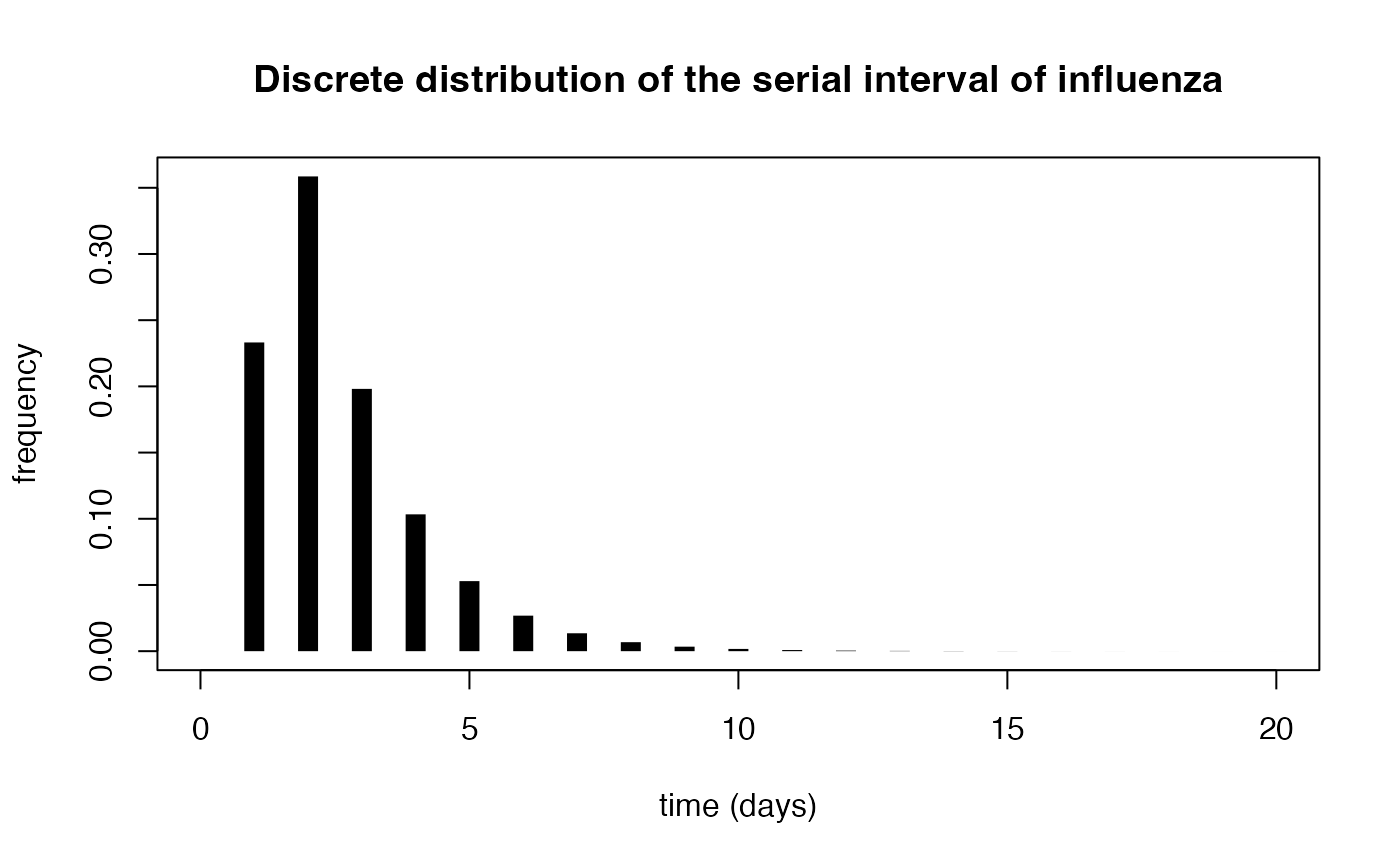
## Computing the discrete serial interval of influenza
mean_flu_si <- 2.6
sd_flu_si <- 1.5
dicrete_si_distr <- discr_si(seq(0, 20), mean_flu_si, sd_flu_si)
plot(seq(0, 20), dicrete_si_distr, type = "h",
          lwd = 10, lend = 1, xlab = "time (days)", ylab = "frequency")
title(main = "Discrete distribution of the serial interval of influenza")