Simple-example • treasure

library(treasure)

This vignette provides a brief example of estimating the number of commodities required for a simple scenario and how these can be converted into costs. We use two small data sets as examples.

Bed nets

First we consider some basic intervention information that includes population at risk (par) and a target level of insecticide treated net (ITN) usage by year.

interventions <- data.frame(
  year = 1:6,
  itn_use = c(0, 0.6, 0.5, 0.2, 0.5, 0.4),
  par = rep(1000, 6)
)
interventions
#>   year itn_use  par
#> 1    1     0.0 1000
#> 2    2     0.6 1000
#> 3    3     0.5 1000
#> 4    4     0.2 1000
#> 5    5     0.5 1000
#> 6    6     0.4 1000

To determine how many nets are required we can use commodity_nets(). Here we assume a constant usage rate, distributions on the first day of each year, and a half life of two years.

dist_steps <- cumsum(c(1, rep(365, 5)))
crop_steps <- dist_steps + 183
half_life  <- 730
use_rate   <- 0.5

interventions$n_nets <- commodity_nets(
  usage = interventions$itn_use,
  use_rate = use_rate,
  distribution_timesteps = dist_steps,
  crop_timesteps = crop_steps,
  half_life = half_life,
  par = interventions$par
)

interventions$cost_nets <- cost_llin(interventions$n_nets)

interventions
#>   year itn_use  par n_nets cost_nets
#> 1    1     0.0 1000      0      0.00
#> 2    2     0.6 1000   1057   3720.64
#> 3    3     0.5 1000    306   1077.12
#> 4    4     0.2 1000      0      0.00
#> 5    5     0.5 1000    839   2953.28
#> 6    6     0.4 1000     29    102.08

barplot(
  interventions$n_nets,
  names.arg = interventions$year,
  col = "#2E86AB",
  border = NA,
  xlab = "Year",
  ylab = "Number of nets"
)

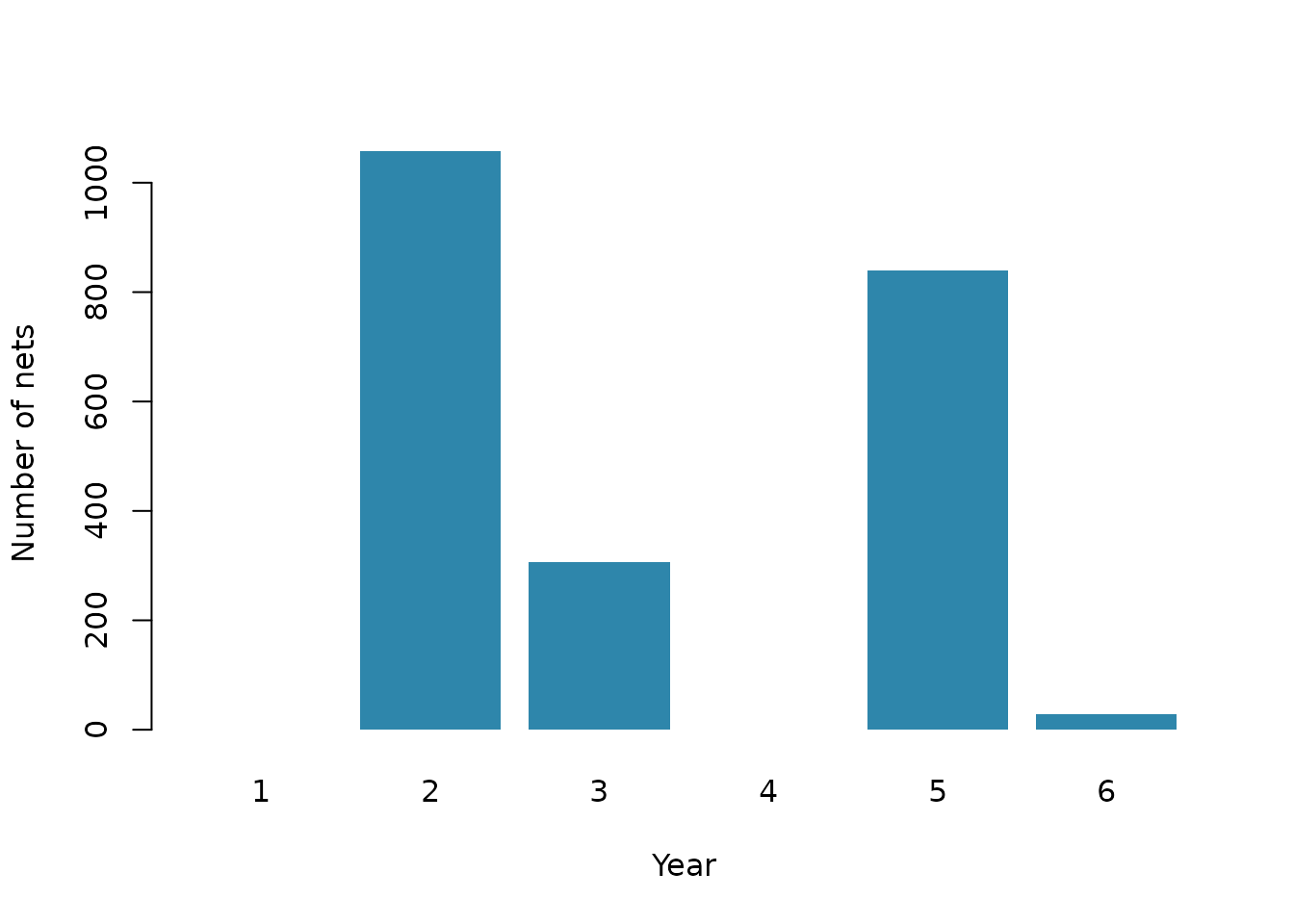
Nets required by year

Cases

The second example uses case data by year and age band. For simplicity we assume constant treatment coverage and diagnostic usage.

cases <- data.frame(
  year = rep(1:6, each = 3),
  age_lower = rep(c(0, 5, 15), 6),
  age_upper = rep(c(5, 15, 100), 6),
  cases = rep(rpois(6, 100), each = 3),
  tx_cov = rep(c(0, 0.3, 0.8), each = 3),
  par = rep(300, 6 * 3)
)
cases
#>    year age_lower age_upper cases tx_cov par
#> 1     1         0         5    85    0.0 300
#> 2     1         5        15    85    0.0 300
#> 3     1        15       100    85    0.0 300
#> 4     2         0         5    89    0.3 300
#> 5     2         5        15    89    0.3 300
#> 6     2        15       100    89    0.3 300
#> 7     3         0         5    99    0.8 300
#> 8     3         5        15    99    0.8 300
#> 9     3        15       100    99    0.8 300
#> 10    4         0         5   106    0.0 300
#> 11    4         5        15   106    0.0 300
#> 12    4        15       100   106    0.0 300
#> 13    5         0         5   111    0.3 300
#> 14    5         5        15   111    0.3 300
#> 15    5        15       100   111    0.3 300
#> 16    6         0         5    81    0.8 300
#> 17    6         5        15    81    0.8 300
#> 18    6        15       100    81    0.8 300

We can estimate the number of rapid diagnostic tests (RDTs) and ACT doses required using commodity_rdt_tests() and commodity_al_doses(). The age specific dose multipliers are determined by the age_upper values.

prop_rdt <- 1
prop_act <- 1

cases$n_rdt <- commodity_rdt_tests(
  n_cases = cases$cases,
  treatment_coverage = cases$tx_cov,
  proportion_rdt = prop_rdt
)

cases$n_act_doses <- commodity_al_doses(
  n_cases = cases$cases,
  treatment_coverage = cases$tx_cov,
  proportion_act = prop_act,
  age_upper = cases$age_upper
)

cases
#>    year age_lower age_upper cases tx_cov par n_rdt n_act_doses
#> 1     1         0         5    85    0.0 300     0           0
#> 2     1         5        15    85    0.0 300     0           0
#> 3     1        15       100    85    0.0 300     0           0
#> 4     2         0         5    89    0.3 300    27         160
#> 5     2         5        15    89    0.3 300    27         400
#> 6     2        15       100    89    0.3 300    27         641
#> 7     3         0         5    99    0.8 300    79         475
#> 8     3         5        15    99    0.8 300    79        1188
#> 9     3        15       100    99    0.8 300    79        1901
#> 10    4         0         5   106    0.0 300     0           0
#> 11    4         5        15   106    0.0 300     0           0
#> 12    4        15       100   106    0.0 300     0           0
#> 13    5         0         5   111    0.3 300    33         200
#> 14    5         5        15   111    0.3 300    33         499
#> 15    5        15       100   111    0.3 300    33         799
#> 16    6         0         5    81    0.8 300    65         389
#> 17    6         5        15    81    0.8 300    65         972
#> 18    6        15       100    81    0.8 300    65        1555

Costs can then be added using the corresponding costing functions.

cases$cost_rdt <- cost_rdt(cases$n_rdt)
cases$cost_act <- cost_al(cases$n_act_doses)
head(cases)
#>   year age_lower age_upper cases tx_cov par n_rdt n_act_doses cost_rdt
#> 1    1         0         5    85    0.0 300     0           0  0.00000
#> 2    1         5        15    85    0.0 300     0           0  0.00000
#> 3    1        15       100    85    0.0 300     0           0  0.00000
#> 4    2         0         5    89    0.3 300    27         160 15.79003
#> 5    2         5        15    89    0.3 300    27         400 15.79003
#> 6    2        15       100    89    0.3 300    27         641 15.79003
#>    cost_act
#> 1   0.00000
#> 2   0.00000
#> 3   0.00000
#> 4  53.06458
#> 5 132.66146
#> 6 212.58999

barplot(
  rbind(cases$n_rdt, cases$n_act_doses),
  beside = TRUE,
  names.arg = cases$year,
  legend.text = c("RDTs", "ACT doses"),
  col = c("#F4A259", "#2E86AB"),
  border = NA,
  xlab = "Year",
  ylab = "Number"
)

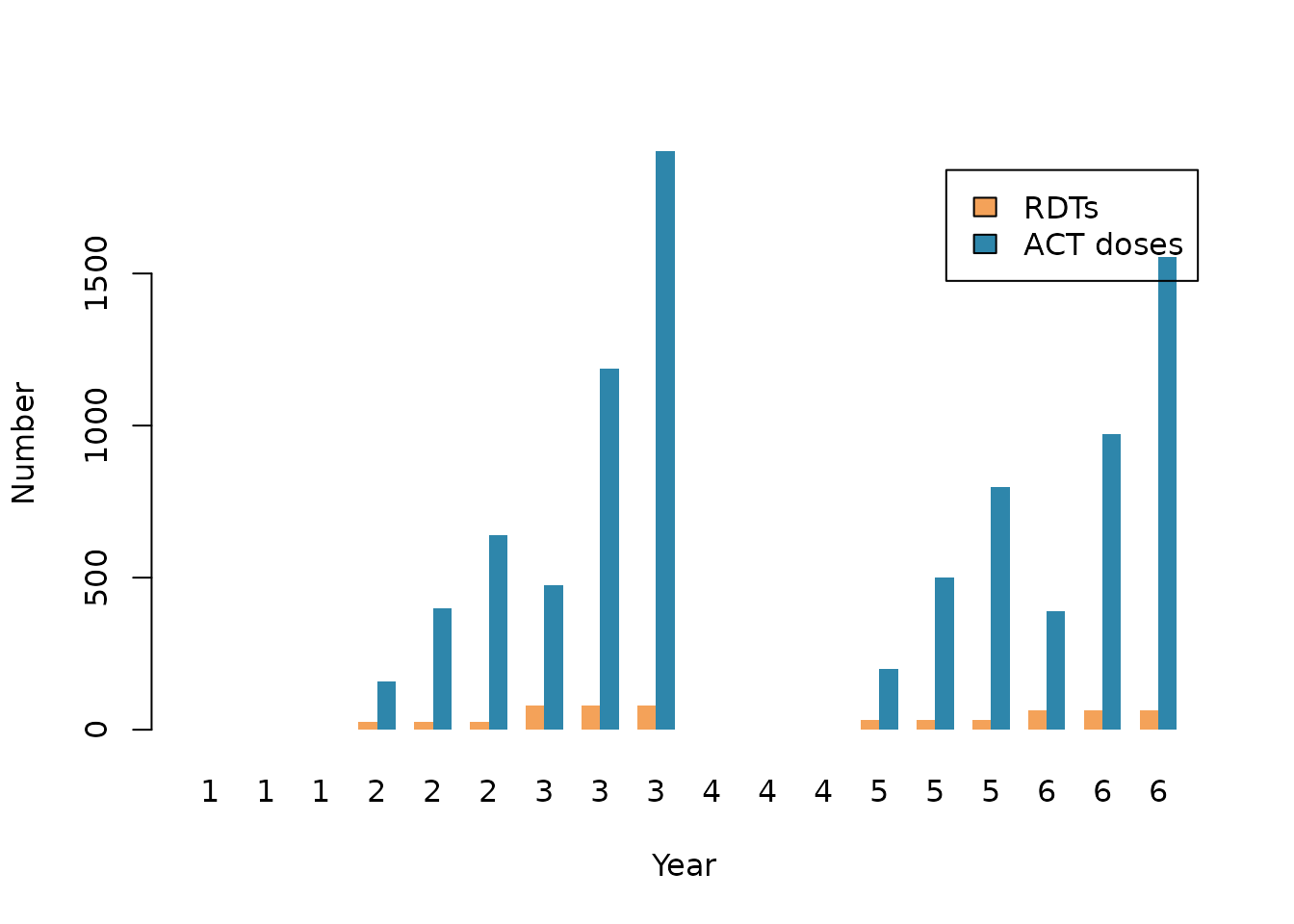
RDTs and ACT doses by year

The examples above show the basic approach for moving from site input and model output data to estimates of commodity requirements and associated costs. More complex scenarios can be handled in the same way by adjusting the input arguments to the commodity and costing functions.