Interpolate the Dormand-Prince output after an integration. This only interpolates the core integration variables and not any additional output variables.
dopri_interpolate(h, t)Arguments
- h
The interpolation history. This can be the output running
dopriwithreturn_history = TRUE, or the history attribute of this object (retrievable withattr(res, "history")).- t
The times at which interpolated output is required. These times must fall within the included history (i.e., the times that the original simulation was run) or an error will be thrown.
Details
This decouples the integration of the equations and the generation of output; it is not necessary for use of the package, but may come in useful where you need to do (for example) root finding on the time course of a problem, or generate minimal output in some cases and interrogate the solution more deeply in others. See the examples and the package vignette for a full worked example.
Examples
# Here is the Lorenz attractor implemented as an R function
lorenz <- function(t, y, p) {
sigma <- p[[1L]]
R <- p[[2L]]
b <- p[[3L]]
c(sigma * (y[[2L]] - y[[1L]]),
R * y[[1L]] - y[[2L]] - y[[1L]] * y[[3L]],
-b * y[[3L]] + y[[1L]] * y[[2L]])
}
# Standard parameters and a reasonable starting point:
p <- c(10, 28, 8 / 3)
y0 <- c(10, 1, 1)
# Run the integration for times [0, 50] and return minimal output,
# but *do* record and return history.
y <- dopri(y0, c(0, 50), lorenz, p,
n_history = 5000, return_history = TRUE,
return_time = FALSE, return_initial = FALSE,
return_by_column = FALSE)
# Very little output is returned (just 3 numbers being the final
# state of the system), but the "history" attribute is fairly
# large matrix of history information. It is not printed though
# as its contents should not be relied on. What does matter is
# the range of supported times printed (i.e., [0, 50]) and the
# number of entries (~2000).
y
#> [,1]
#> [1,] 4.715752
#> [2,] 7.090322
#> [3,] 17.008255
#> attr(,"history")
#> <dopri_history>
#> - equations: 3
#> - time: [0, 50]
#> - entries: 2128
#> - order: 5
# Generate an interpolated set of variables using this; first for
# 1000 steps over the full range:
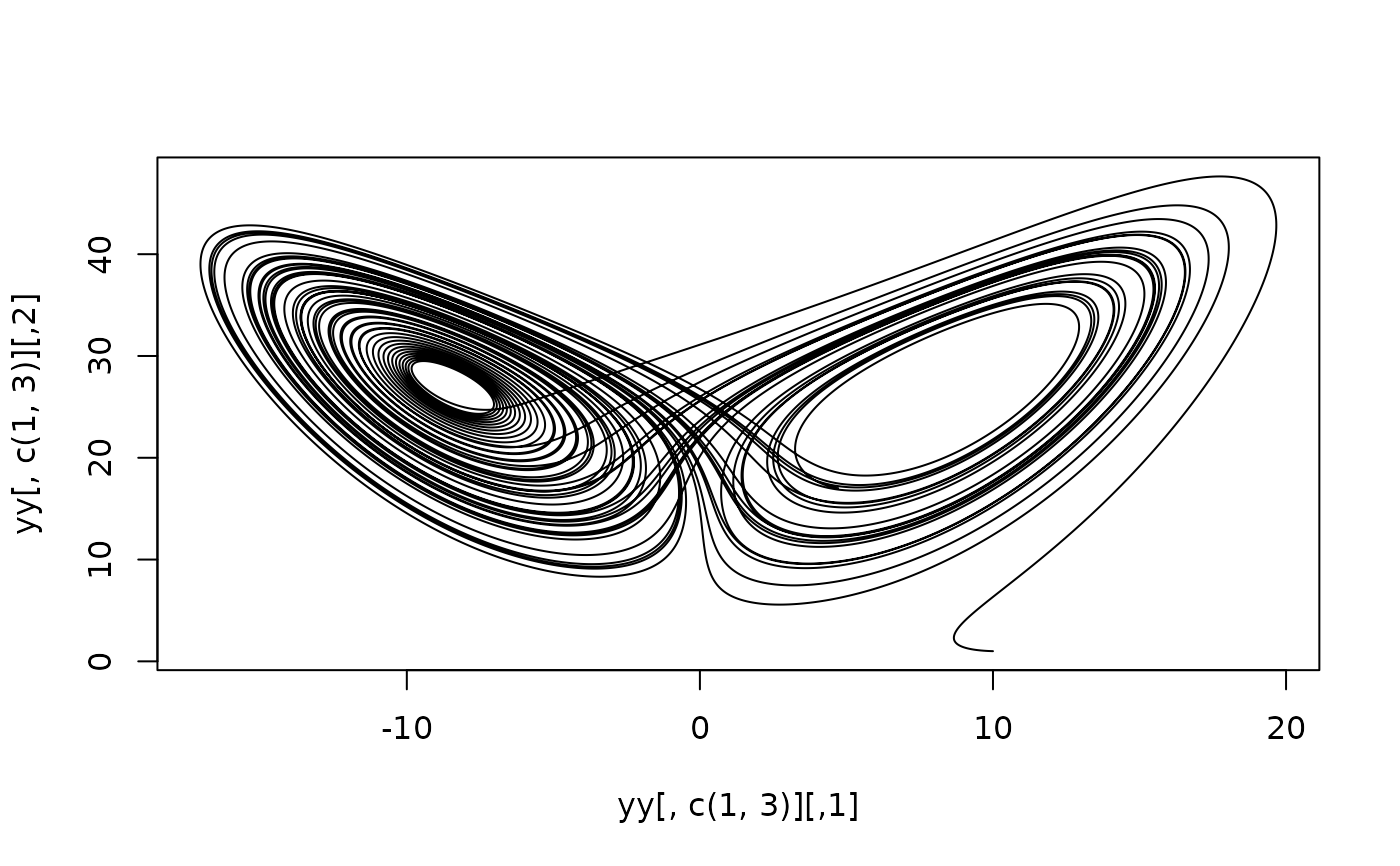
tt <- seq(0, 50, length.out = 1000)
yy <- dopri_interpolate(y, tt)
plot(yy[, c(1, 3)], type = "l")
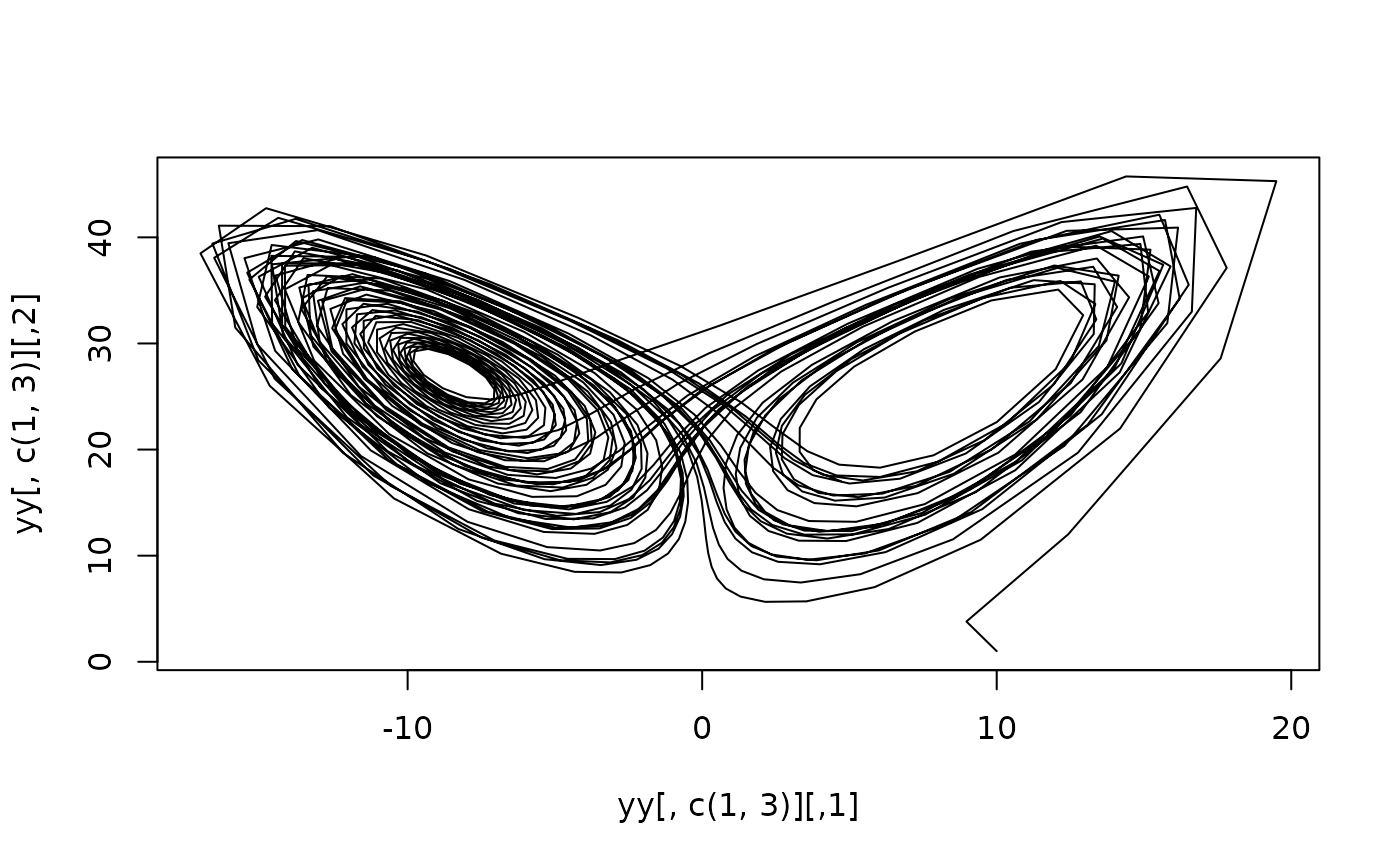 # Then for 50000
tt <- seq(0, 50, length.out = 50000)
yy <- dopri_interpolate(y, tt)
plot(yy[, c(1, 3)], type = "l")
# Then for 50000
tt <- seq(0, 50, length.out = 50000)
yy <- dopri_interpolate(y, tt)
plot(yy[, c(1, 3)], type = "l")