Integrate ODE/DDE with dopri

Integrate an ODE or DDE with dopri.

dopri(y, times, func, parms, ..., n_out = 0L, output = NULL,
  rtol = 1e-06, atol = 1e-06, step_size_min = 0, step_size_max = Inf,
  step_size_initial = 0, step_max_n = 100000L,
  step_size_min_allow = FALSE, tcrit = NULL, event_time = NULL,
  event_function = NULL, method = "dopri5", stiff_check = 0,
  verbose = FALSE, callback = NULL, n_history = 0,
  grow_history = FALSE, return_history = n_history > 0, dllname = "",
  parms_are_real = TRUE, ynames = names(y), outnames = NULL,
  return_by_column = TRUE, return_initial = TRUE, return_time = TRUE,
  return_output_with_y = TRUE, return_statistics = FALSE,
  restartable = FALSE, return_minimal = FALSE)

dopri5(y, times, func, parms, ...)

dopri853(y, times, func, parms, ...)

dopri_continue(obj, times, y = NULL, ..., copy = FALSE, parms = NULL,
  tcrit = NULL, return_history = NULL, return_by_column = NULL,
  return_initial = NULL, return_statistics = NULL, return_time = NULL,
  return_output_with_y = NULL, restartable = NULL)

ylag(t, i = NULL)

Arguments

y: Initial conditions for the integration
times: Times where output is needed. Unlike deSolve we won't actually stop at these times, but instead interpolate back to get the result.
func: Function to integrate. Can be an R function of arguments t, y, parms, returning a numeric vector, or it can be the name or address of a C function with arguments size_t n, double t, const double *y, double *dydt, void *data.
parms: Parameters to pass through to the derivatives.
...: Dummy arguments - nothing is allowed here, but this means that all further arguments must be specified by name (not order) so I can easily reorder them later on.
n_out: Number of "output" variables (not differential equation variables) to compute via the routine output.
output: The output routine; either an R function taking arguments t, y, parms or the name/address of a C function taking arguments size_t n, double t, const double *y, size_t n_out, double *out, void *data.
rtol: The per-step relative tolerance. The total accuracy will be less than this.
atol: The per-step absolute tolerance.
step_size_min: The minimum step size. The actual minimum used will be the largest of the absolute value of this step_size_min or .Machine$double.eps. If the integration attempts to make a step smaller than this, it will throw an error by default, stopping the integration (note that this differs from the treatment of hmin in deSolve::lsoda). See allow_step_size_min to change this behaviour.
step_size_max: The largest step size. By default there is no maximum step size (Inf) so the solver can take as large a step as it wants to. If you have short-lived fluctuations in your rhs that the solver may skip over by accident, then specify a smaller maximum step size here (or use tcrit below).
step_size_initial: The initial step size. By default the integrator will guess the step size automatically, but one can be given here instead.
step_max_n: The maximum number of steps allowed. If the solver takes more steps than this it will throw an error. Note the number of evaluations of func will be about 6 times the number of steps (or 11 times if using method = "dopri853").
step_size_min_allow: Logical, indicating if when a step size is driven down to step_size_min we should allow it to proceed. This is the behaviour in of hmin in deSolve::lsoda.
tcrit: An optional vector of critical times that the solver must stop at (rather than interpolating over). This can include an end time that we can't go past, or points within the integration that must be stopped at exactly (for example cases where the derivatives change abruptly). Note that this differs from the interpretation of this parameter in deSolve; there tcrit is a single time that integration may not go past – with dde we never go past the final time, and this is just for times that fall within the range of times in times.
event_time: Vector of times to fire events listed in event_function at
event_function: Function to fire at events. For R models (func is an R function and dllname is empty), this must be either a single R function (same function for all events) or a list of R functions. For C models, this must be a singe C function (same requirements as func or output or a list/vector of these as appropriate).
method: The integration method to use, as a string. The supported methods are "dopri5" (5th order method with 4th order dense output) and "dopri853" (8th order method with 7th order output and embedded 5th and 3rd order schemes). Alternatively, use the functions dopri5 or dopri853 which simply sets this argument.
stiff_check: How often to check that the problem has become stiff. If zero, then the problem is never checked, and if positive then the problem is checked every stiff_check accepted steps. The actual check is based off the algorithm in Hairer's implementation of the solvers and may be overly strict, especially for delay equations with the 853 method (in my limited experience with it).
verbose: Be verbose, and print information about each step. This may be useful for learning about models that misbehave. Valid values are TRUE (enable debugging) or FALSE (disable debugging) or use one of dopri:::VERBOSE_QUIET, dopri:::VERBOSE_STEP or VERBOSE:::VERBOSE_EVAL. If an R function is provided as the argument callback then this function will also be called at each step or evaluation (see below for details).
callback: Callback function that can be used to make verbose output more useful. This can be used to return more information about the evaluation as it proceeds, generally as information printed to the screen. The function must accept arguments t, y and dydt. See Details for further information.
n_history: Number of history points to retain. This needs to be greater than zero for delay differential equations to work. Alternatively, this may be greater than zero to return model outputs that can be inspected later.
grow_history: Logical indicating if history should be grown during the simulation. If FALSE (the default) then when history is used it is overwritten as needed (so only the most recent n_history elements are saved. This may require some tuning so that you have enough history to run your simulation (i.e. to the longest delay) or an error will be thrown when it underflows. The required history length will vary with your delay sizes and with the timestep for dopri. If TRUE, then history will grow as the buffer is exhausted. The growth is geometric, so every time it reaches the end of the buffer it will increase by a factor of about 1.6 (see the ring documentation). This may consume more memory than necessary, but may be useful where you don't want to care about picking the history length carefully.
return_history: Logical indicating if history should be returned alongside the output or discarded. By default, history is retained if n_history is greater than 0, but that might change (and may not be desirable unless you plan on actually using it).
dllname: Name of the shared library (without extension) to find the function func (and output if given) in the case where func refers to compiled function.
parms_are_real: Logical, indicating if parms should be treated as vector of doubles by func (when it is a compiled function). If TRUE (the default), then REAL(parms), which is double* is passed through. If FALSE then if params is an externalptr type (EXTPTRSXP) we pass through the result of R_ExternalPtrAddr, otherwise we pass params through unmodified as a SEXP. In the last case, in your target function you will need to include <Rinternals.h>, cast to SEXP and then pull it apart using the R API (or Rcpp).
ynames: Logical, indicating if the output should be named following the names of the input vector y. Alternatively, if ynames is a character vector of the same length as y, these will be used as the output names.
outnames: An optional character vector, used when n_out is greater than 0, to name the model output matrix.
return_by_column: Logical, indicating if the output should be returned organised by column (rather than row). This incurs a slight cost for transposing the matrices. If you can work with matrices that are transposed relative to deSolve, then set this to FALSE.
return_initial: Logical, indicating if the output should include the initial conditions. Specifying FALSE avoids binding this onto the output.
return_time: Logical, indicating if a row (or column if return_by_column is TRUE) representing time is included. If FALSE, this is not added.
return_output_with_y: Logical, indicating if the output should be bound together with the returned matrix y (as it is with deSolve). If FALSE, then output will be returned as the attribute output.
return_statistics: Logical, indicating if statistics about the run should be included. If TRUE, then an integer vector containing the number of target evaluations, steps, accepted steps and rejected steps is returned (the vector is named).
restartable: Logical, indicating if the problem should be restartable. If TRUE, then the return value of an integration can be passed to dopri_restart to continue the integration after arbitrary changes to the state or the parameters. Note that when using delay models, the integrator is fairly naive about how abrupt changes in the state space are dealt with, and may perform very badly with method = "dopri853" which assumes a fairly smooth problem. Note that this is really only useful for delay differential equations where you want to keep the history but make changes to the parameters or to the state vector while keeping the history of the problem so far.
return_minimal: Shorthand option - if set to TRUE then it sets all of return_by_column, return_initial, return_time, return_output_with_y to FALSE
obj: An object to continue from; this must be the results of running an integration with the option restartable = TRUE. Note that continuing a problem moves the pointer along in time (unless copy = TRUE, and that the incoming time (times[[1]]) must equal the previous time exactly.
copy: Logical, indicating if the pointer should be copied before continuing. If TRUE, this is non-destructive with respect to the data in the original pointer so the problem can be restarted multiple times. By default this is FALSE because there is a (potentially very small) cost to this operation.
t: The time to access (not that this is not an offset, but the actual time; within your target function you'd write things like tlag(t - 1) to get 1 time unit ago.
i: index within the state vector y to return. The index here is R-style base-1 indexing, so pass 1 in to access the first element. This can be left NULL to return all the elements or a vector longer than one.

Value

At present the return value is transposed relative to deSolve. This might change in future.

Details

Like deSolve::lsoda, this function has many arguments. This is far from ideal, and I would welcome any approach for simplifying it a bit.

The options return_by_column, return_initial, return_time, return_output_with_y exist because these options all carry out modifications of the data at the end of solving the ODE and this can incur a small but measurable cost. When solving an ODE repeatedly (e.g., in the context of an MCMC or optimisation) it may be useful to do as little as possible. For simple problems this can save around 5-10% of the total computational time (especially the transpose). The shorthand option return_minimal will set all to FALSE when used.

Verbose output and callbacks

Debugging a failed integration can be difficult, but dopri provides a couple of tools to get more information about where a failure might have occurred. Most simply, one can pass verbose = TRUE which will print information about the time and the step size at each point just before the step is stated. Passing in verbose = dde:::VERBOSE_EVAL will print information just before every evaluation of the target function (there are several evaluations per step).

However, this does not provide information about the state just before failure. To get that, one must provide a callback function - this is an R function that will be called just before a step or evaluation (based on the value of the verbose argument) in place of the default print. Define a callback function with arguments t, h and y where t is the time (beginning of a step or location of an evaluation), h is the step size (or NA for an evaluation) and y is the state at the point of the step or evaluation. Your callback function can do anything - you can print to the screen (using cat or message), you can store results using a closure and <<- or you could conditionally use a browser() call to debug interactively. However, it is not possible for the callback to affect the solution short of throwing an error and interrupting it. See the Examples for an example of use.

Examples


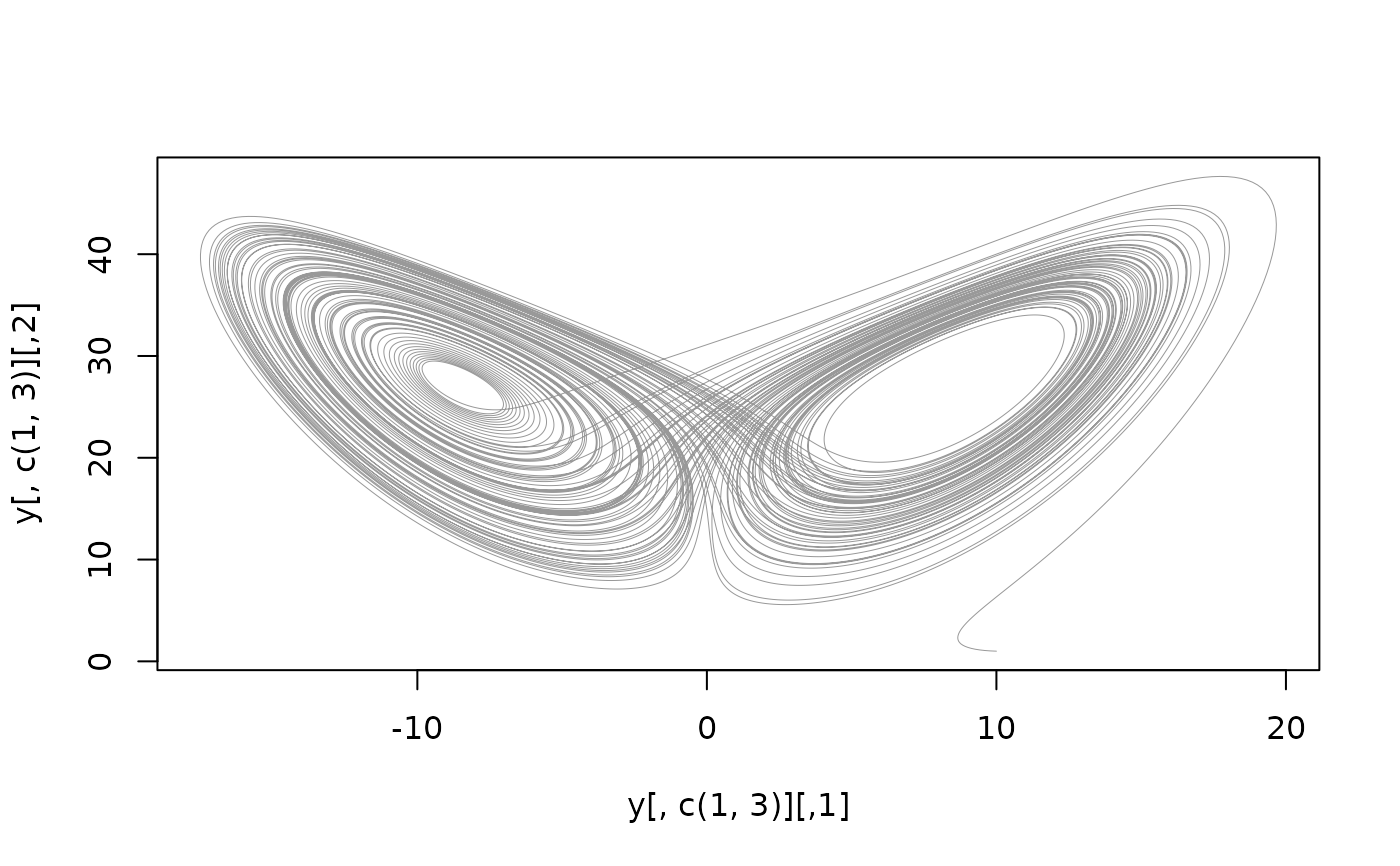
# The lorenz attractor:
lorenz <- function(t, y, p) {
  sigma <- p[[1L]]
  R <- p[[2L]]
  b <- p[[3L]]
  c(sigma * (y[[2L]] - y[[1L]]),
    R * y[[1L]] - y[[2L]] - y[[1L]] * y[[3L]],
    -b * y[[3L]] + y[[1L]] * y[[2L]])
}

p <- c(10, 28, 8 / 3)
y0 <- c(10, 1, 1)

tt <- seq(0, 100, length.out = 40000)
y <- dde::dopri(y0, tt, lorenz, p, return_time = FALSE)
plot(y[, c(1, 3)], type = "l", lwd = 0.5, col = "#00000066")


# If we want to print progress as the integration progresses we can
# use the verbose argument:
y <- dde::dopri(y0, c(0, 0.1), lorenz, p, verbose = TRUE)
#> [step] t: 0.000000, h: 5.537306e-03
#> [step] t: 0.005537, h: 6.430928e-03
#> [step] t: 0.011968, h: 8.739468e-03
#> [step] t: 0.020708, h: 9.809251e-03
#> [step] t: 0.030517, h: 1.107340e-02
#> [step] t: 0.041590, h: 1.205421e-02
#> [step] t: 0.053645, h: 1.314483e-02
#> [step] t: 0.066789, h: 1.425269e-02
#> [step] t: 0.081042, h: 1.540209e-02
#> [step] t: 0.096444, h: 3.555820e-03

# Or print the y values too using a callback:
callback <- function(t, h, y) {
  message(sprintf("t: %f, h: %e, y: [%s]", t, h,
                  paste(format(y, 5), collapse = ", ")))
}
y <- dde::dopri(y0, c(0, 0.1), lorenz, p, verbose = TRUE,
                callback = callback)
#> t: 0.000000, h: 5.537306e-03, y: [10, 1, 1]
#> t: 0.005537, h: 6.430928e-03, y: [9.554934, 2.449143, 1.078091]
#> t: 0.011968, h: 8.739468e-03, y: [9.162942, 4.041912, 1.253444]
#> t: 0.020708, h: 9.809251e-03, y: [8.821880, 6.082211, 1.617623]
#> t: 0.030517, h: 1.107340e-02, y: [8.669544, 8.247306, 2.182106]
#> t: 0.041590, h: 1.205421e-02, y: [8.750993, 10.588819, 3.012980]
#> t: 0.053645, h: 1.314483e-02, y: [9.103806, 13.068684, 4.169498]
#> t: 0.066789, h: 1.425269e-02, y: [9.760060, 15.730374, 5.779677]
#> t: 0.081042, h: 1.540209e-02, y: [10.746777, 18.566823, 8.024051]
#> t: 0.096444, h: 3.555820e-03, y: [12.07997, 21.49481, 11.15596]