Advanced_calibration
Advanced_calibration.RmdWe’ve seen how to perform a very simple calibration. Here we will look at more advanced options. To start with lets define a new summary function, this one will produce a vector of annual average estimates of prevalence in 2-10 year olds:
annual_pfpr_summary <- function(x){
year <- ceiling(x$timestep / 365)
pfpr <- x$n_detect_lm_730_3650 / x$n_age_730_3650
tapply(pfpr, year, mean)
}We can use this function to calibrate against multiple years of PfPr estimates:
target <- c(0.3, 0.2, 0.1)
parameters <- get_parameters() |>
set_bednets(
timesteps = 365 * 0:2,
coverages = c(0, 0.3, 0.4),
retention = 5 * 365,
dn0 = matrix(0.53, nrow = 3, ncol = 1),
rn = matrix(0.56, nrow = 3, ncol = 1),
rnm = matrix(0.24, nrow = 3, ncol = 1),
gamman = rep(2.64 * 365, 3)
)
parameters$timesteps <- 365 * 3
set.seed(123)
out <- calibrate(
parameters = parameters,
target = target,
summary_function = annual_pfpr_summary,
eq_prevalence = target[1]
)
#> Initialising EIR
#> Slice sampling EIR, side 1
#> Attempt 1 of 10
#>
#>
#> Current Target
#> -------- -------
#> 0.32 0.3
#> 0.24 0.2
#> 0.11 0.1
#>
#>
#>
#> EIR Objective
#> ---- ----------
#> 4.4 0.065
#> 0.0 NA
#> Slice sampling EIR, side 2
#> Attempt 2 of 10
#>
#>
#> Current Target
#> -------- -------
#> 0.200 0.3
#> 0.130 0.2
#> 0.075 0.1
#>
#>
#>
#> EIR Objective
#> ---- ----------
#> 4.4 0.065
#> 2.7 -0.200
#> Success
parameters$human_population <- 5000
parameters <- set_equilibrium(parameters, init_EIR = out)
raw <- run_simulation(parameters$timesteps + 100, parameters = parameters)
raw$pfpr <- raw$n_detect_lm_730_3650 / raw$n_age_730_3650
ggplot() +
geom_point(aes(x = 365 * (0:2 + 0.5), y = target), col = "dodgerblue", size = 4) +
geom_line(data = raw, aes(x = timestep, y = pfpr), col = "deeppink", linewidth = 1) +
ylim(0, 1) +
ylab(expression(italic(Pf)*Pr[2-10])) +
xlab("Time") +
theme_bw()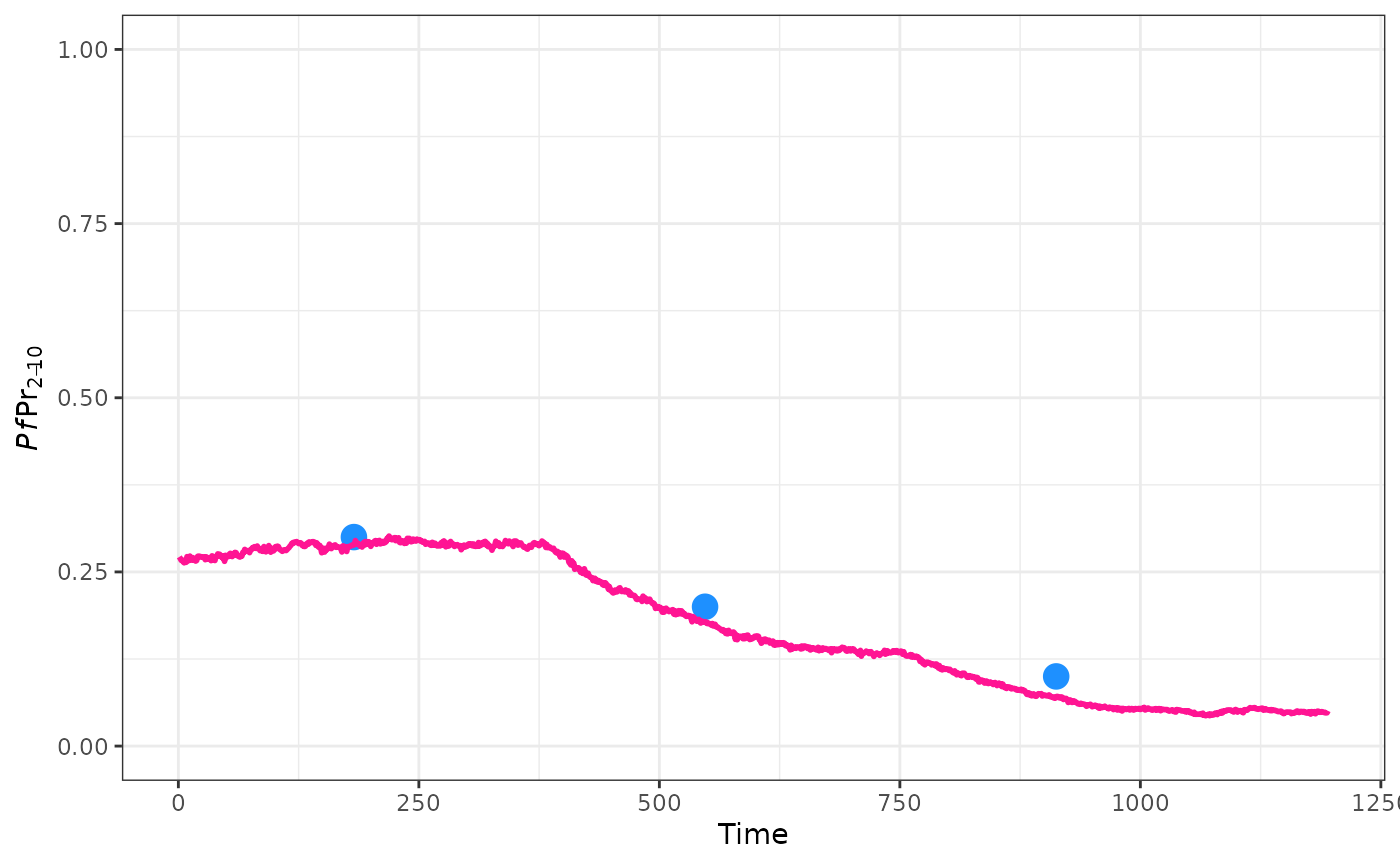
Population size
There is no single correct answer to the question “what modelled
population size should I use?”. In our pursuit of efficiency during the
calibration process, it is our preference to begin with a modestly sized
modelled population. This approach, however, requires a balance: the
population must be sufficiently large to ensure that the level of
stochastic noise remains within acceptable bounds and avoid unwanted
elimination due to stochastic fade-out. If unwanted elimination occurs
(where any output = 0 and taregt != 0), the algoritm will first increase
the human population size to the subsequent larger value specified in
the human_population argument.
You must be happy with the level of stochastic in a run with the
smallest values in the human_popualation argument.
We can see this occuring below:
# Define target, here a prevalence measures:
target <- 0.001
parameters <- get_parameters()
parameters$timesteps <- 365 * 3
set.seed(123)
out <- calibrate(
parameters = parameters,
target = target,
summary_function = summary_mean_pfpr_2_10,
eq_prevalence = target,
human_population = c(100, 1000, 10000)
)
#> Initialising EIR
#> Slice sampling EIR, side 1
#> Attempt 1 of 10
#>
#>
#> Current Target
#> -------- -------
#> 0 0.001
#>
#>
#>
#> EIR Objective
#> ------- ----------
#> 0.0055 NA
#> 0.0000 NA
#> Increasing human population due to elimination
#> Running with new population size: 1000
#> Attempt 2 of 10
#>
#>
#> Current Target
#> -------- -------
#> 0.0029 0.001
#>
#>
#>
#> EIR Objective
#> ------- ----------
#> 0.0055 0.0019
#> 0.0000 NA
#> Slice sampling EIR, side 2
#> Attempt 3 of 10
#>
#>
#> Current Target
#> -------- -------
#> 5.8e-05 0.001
#>
#>
#>
#> EIR Objective
#> ------- ----------
#> 0.0055 0.00190
#> 0.0034 -0.00094
#> SuccessEIR initialisation
To provide a reasonable starting guess for the calibration, we use
the malaria model equilibrium solution to match to a baseline PfPr
eq_prevalence given a level of treatment coverage
eq_ft. A good initialised EIR will mean that the algorithm
converges more quickly, but isn’t necessary. If you don’t know
eq_prevalence or eq_ft, try with a reasonable
guess.
Weighting target values
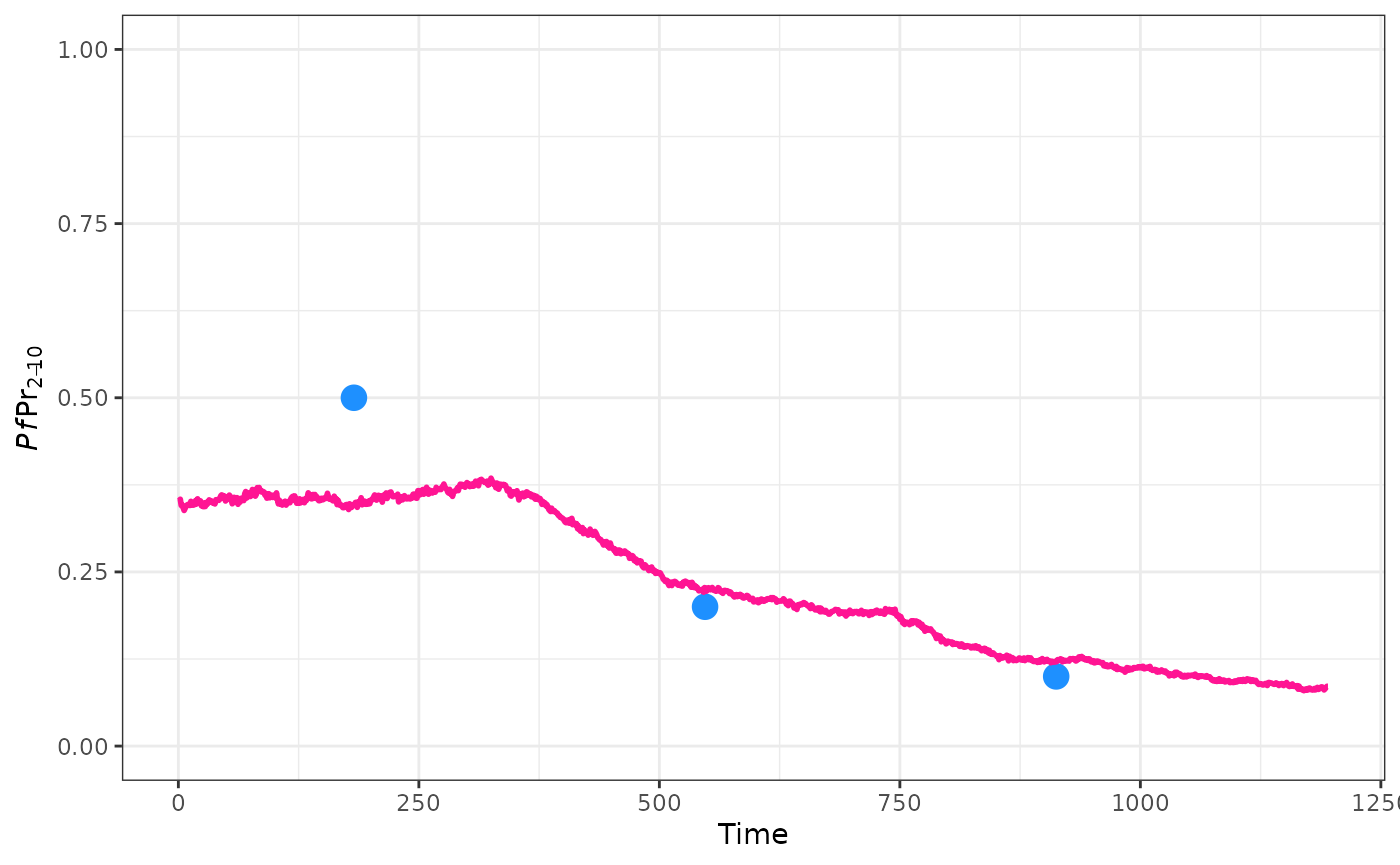
There may be a situation where there is more evidence to support some specific target data over other. In this situation we can weight our target and summary function to bias our fitting more towards or away from certain points.
target <- c(0.5, 0.2, 0.1)
weights = c(0.1, 1, 1)
weighted_target <- target * weights
weighted_annual_pfpr_summary <- function(x, w = weights){
year <- ceiling(x$timestep / 365)
pfpr <- x$n_detect_lm_730_3650 / x$n_age_730_3650
tapply(pfpr, year, mean) * w
}
parameters <- get_parameters() |>
set_bednets(
timesteps = 365 * 0:2,
coverages = c(0, 0.3, 0.4),
retention = 5 * 365,
dn0 = matrix(0.53, nrow = 3, ncol = 1),
rn = matrix(0.56, nrow = 3, ncol = 1),
rnm = matrix(0.24, nrow = 3, ncol = 1),
gamman = rep(2.64 * 365, 3)
)
parameters$timesteps <- 365 * 3
set.seed(123)
out <- calibrate(
parameters = parameters,
target = weighted_target,
summary_function = weighted_annual_pfpr_summary,
eq_prevalence = target[1]
)
#> Initialising EIR
#> Slice sampling EIR, side 1
#> Attempt 1 of 10
#>
#>
#> Current Target
#> -------- -------
#> 0.05 0.05
#> 0.35 0.20
#> 0.18 0.10
#>
#>
#>
#> EIR Objective
#> ---- ----------
#> 15 0.24
#> 0 NA
#> Slice sampling EIR, side 2
#> Attempt 2 of 10
#>
#>
#> Current Target
#> -------- -------
#> 0.037 0.05
#> 0.280 0.20
#> 0.120 0.10
#>
#>
#>
#> EIR Objective
#> ---- ----------
#> 15 0.24
#> 9 0.09
#> Attempt 3 of 10
#>
#>
#> Current Target
#> -------- -------
#> 0.033 0.05
#> 0.190 0.20
#> 0.090 0.10
#>
#>
#>
#> EIR Objective
#> ---- ----------
#> 9.0 0.090
#> 5.5 -0.039
#> Success
parameters$human_population <- 5000
parameters <- set_equilibrium(parameters, init_EIR = out)
raw <- run_simulation(parameters$timesteps + 100, parameters = parameters)
raw$pfpr <- raw$n_detect_lm_730_3650 / raw$n_age_730_3650
ggplot() +
geom_point(aes(x = 365 * (0:2 + 0.5), y = target), col = "dodgerblue", size = 4) +
geom_line(data = raw, aes(x = timestep, y = pfpr), col = "deeppink", linewidth = 1) +
ylim(0, 1) +
ylab(expression(italic(Pf)*Pr[2-10])) +
xlab("Time") +
theme_bw()