Fitting odin models with monty
A pragmatic introduction
Previously, on “Introduction to odin”
- We created some simple compartmental models
- We ran these and observed trajectories over time
- We saw that stochastic models produce a family of trajectories
Our model
update(S) <- S - n_SI
update(I) <- I + n_SI - n_IR
update(R) <- R + n_IR
update(incidence) <- incidence + n_SI
initial(S) <- N - I0
initial(I) <- I0
initial(R) <- 0
initial(incidence, zero_every = 1) <- 0
p_SI <- 1 - exp(-beta * I / N * dt)
p_IR <- 1 - exp(-gamma * dt)
n_SI <- Binomial(S, p_SI)
n_IR <- Binomial(I, p_IR)
N <- parameter(1000)
I0 <- parameter(10)
beta <- parameter(0.2)
gamma <- parameter(0.1)Example output
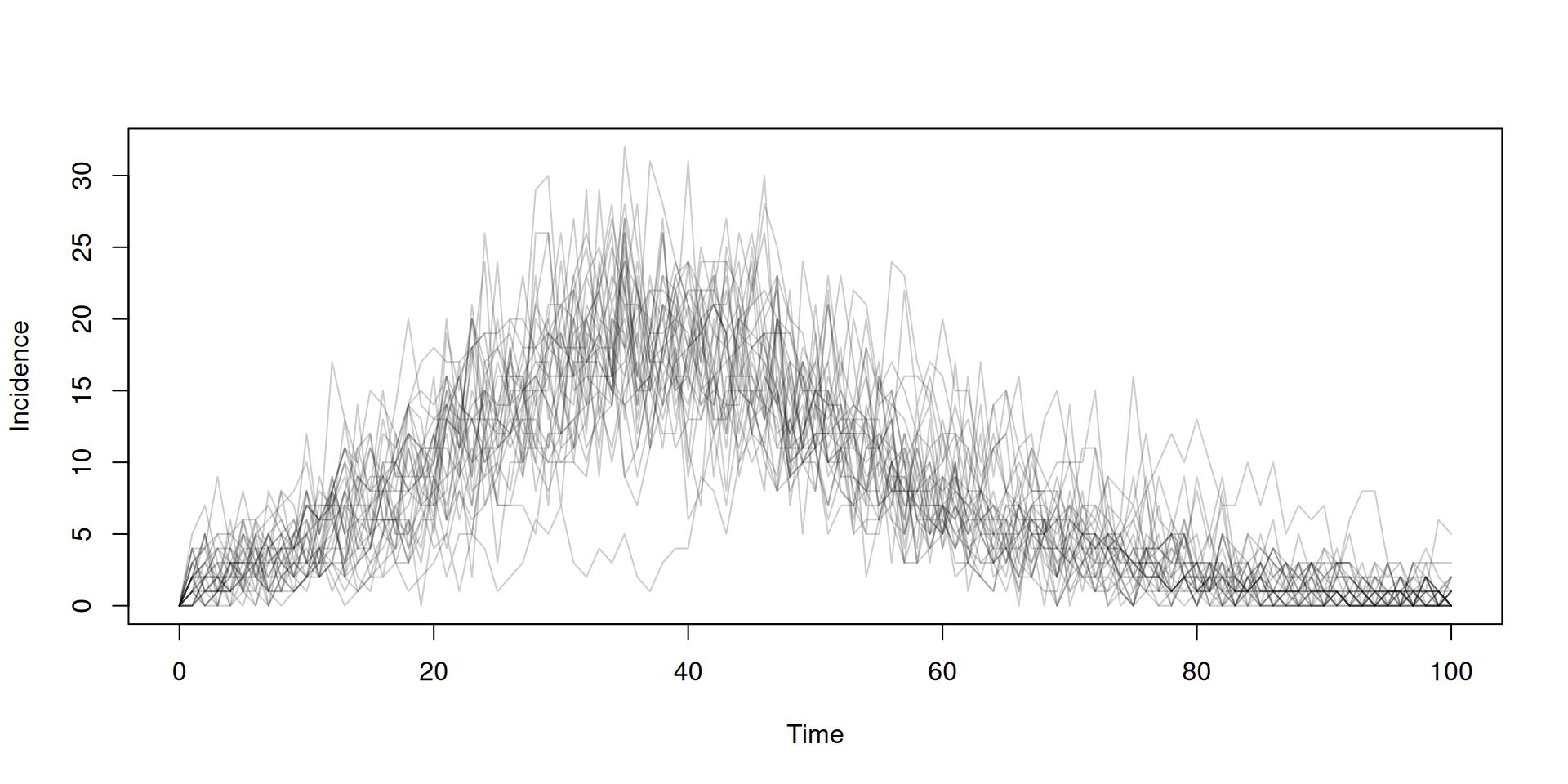
How do we fit this to data?
We need:
- a data set
- time series of observed data (incidence? prevalence? something else?)
- a measure of goodness of fit
- how do we cope with stochasticity?
- to know what parameters we are trying to fit
The data
You should download incidence.csv
We will fit cases here to incidence in our model.
The data
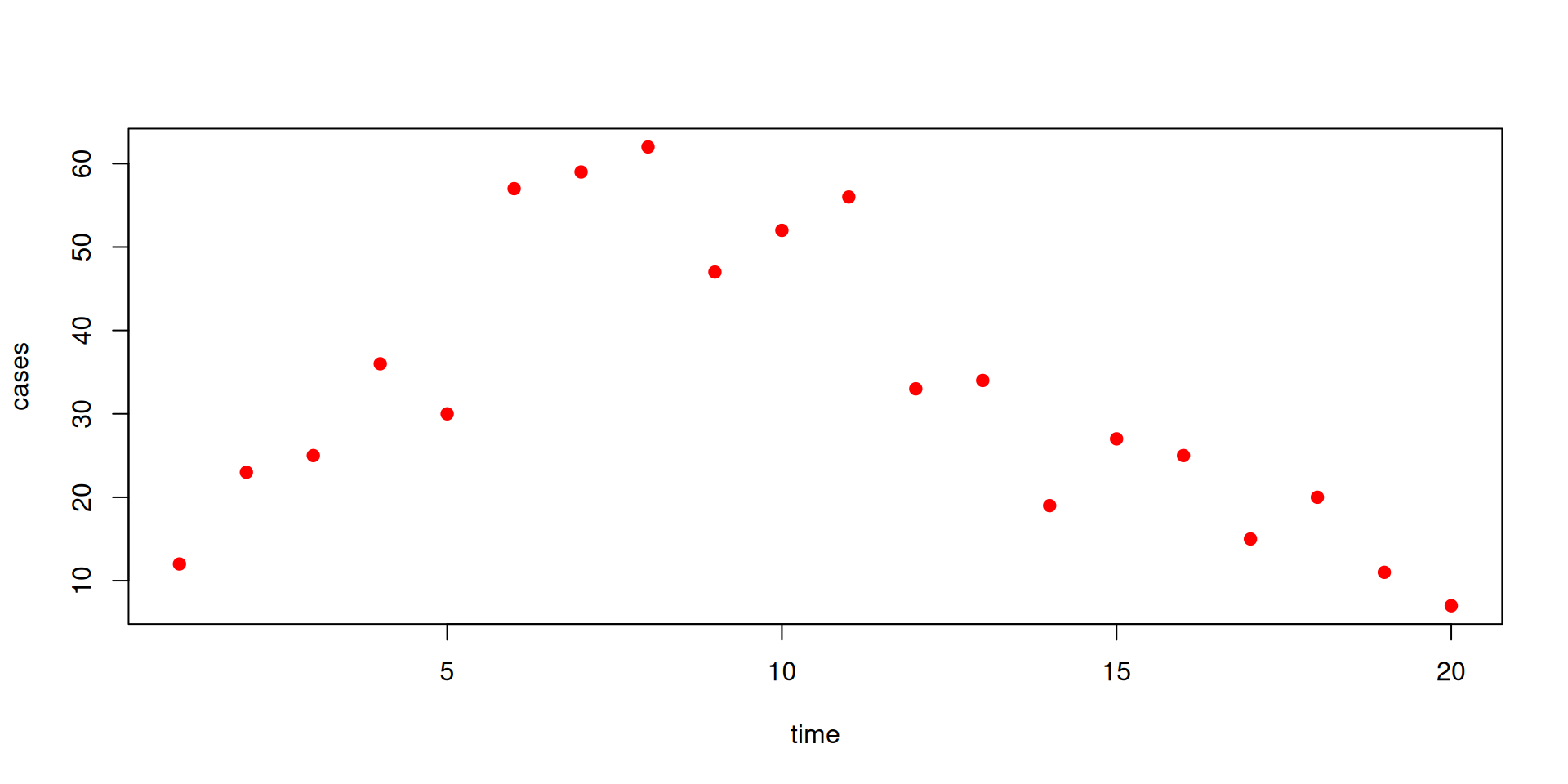
Measuring goodness of fit
Run the system with beta = 0.4 and gamma = 0.2
Measuring goodness of fit
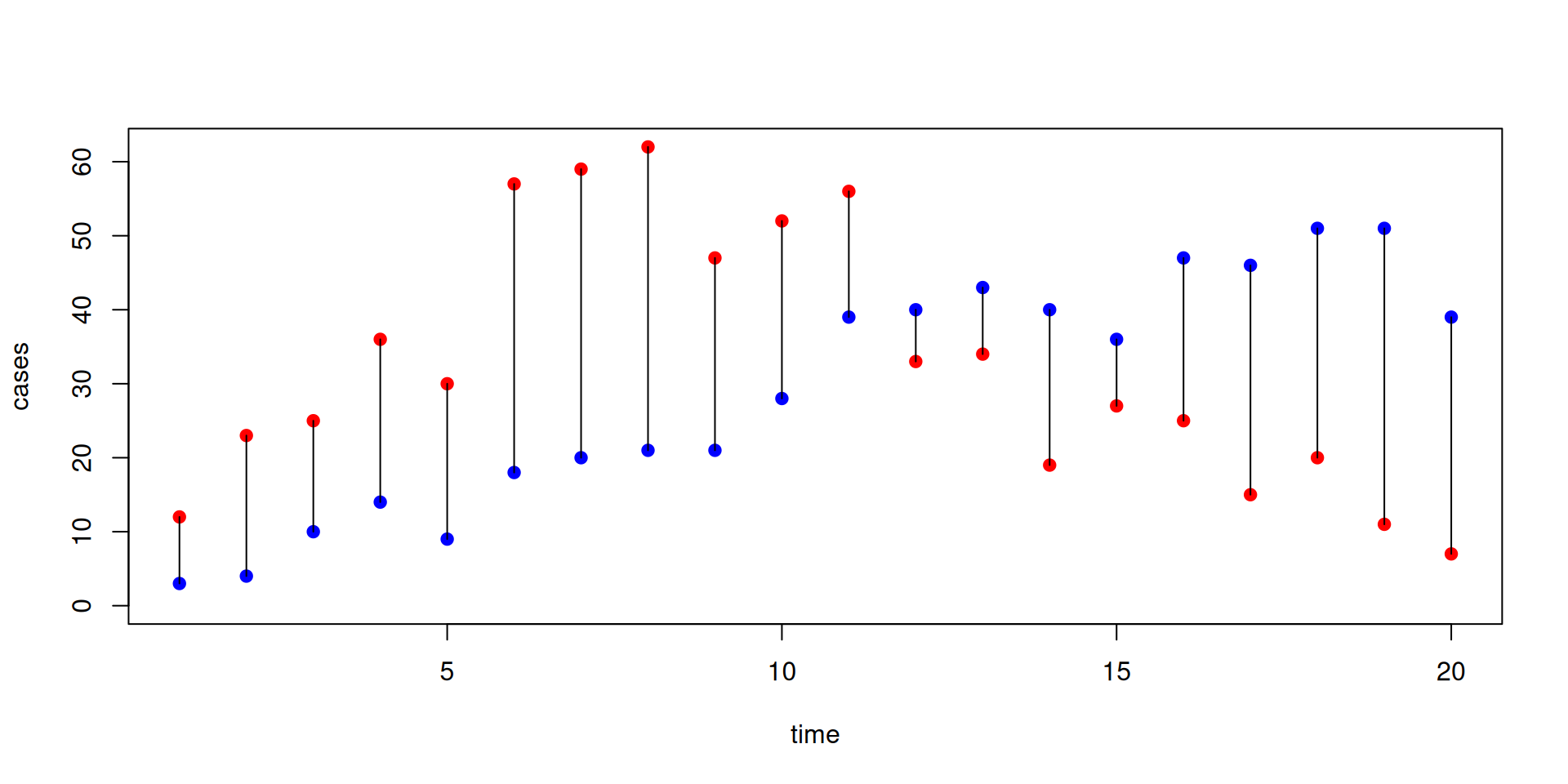
Measuring goodness of fit
\[ \Pr(\mathrm{data} | \mathrm{model}) \]
perhaps:
\[ \Pr(\mathrm{observed\ cases}) \sim \mathrm{Poisson}(\mathrm{modelled\ cases}) \]
Adding goodness-of-fit to the model
update(S) <- S - n_SI
update(I) <- I + n_SI - n_IR
update(R) <- R + n_IR
update(incidence) <- incidence + n_SI
initial(S) <- N - I0
initial(I) <- I0
initial(R) <- 0
initial(incidence, zero_every = 1) <- 0
p_SI <- 1 - exp(-beta * I / N * dt)
p_IR <- 1 - exp(-gamma * dt)
n_SI <- Binomial(S, p_SI)
n_IR <- Binomial(I, p_IR)
N <- parameter(1000)
I0 <- parameter(10)
beta <- parameter(0.2)
gamma <- parameter(0.1)
cases <- data()
cases ~ Poisson(incidence)Measuring goodness-of-fit
Filtered trajectories
dust_likelihood_run(filter, list(beta = 0.4, gamma = 0.2),
save_trajectories = TRUE, index_state = idx)
#> [1] -115.1948
y <- dust_likelihood_last_trajectories(filter)
matplot(data$time, t(drop(y)), type = "l", col = "#00000033", lty = 1,
xlab = "Time", ylab = "Incidence")
points(data, pch = 19, col = "red")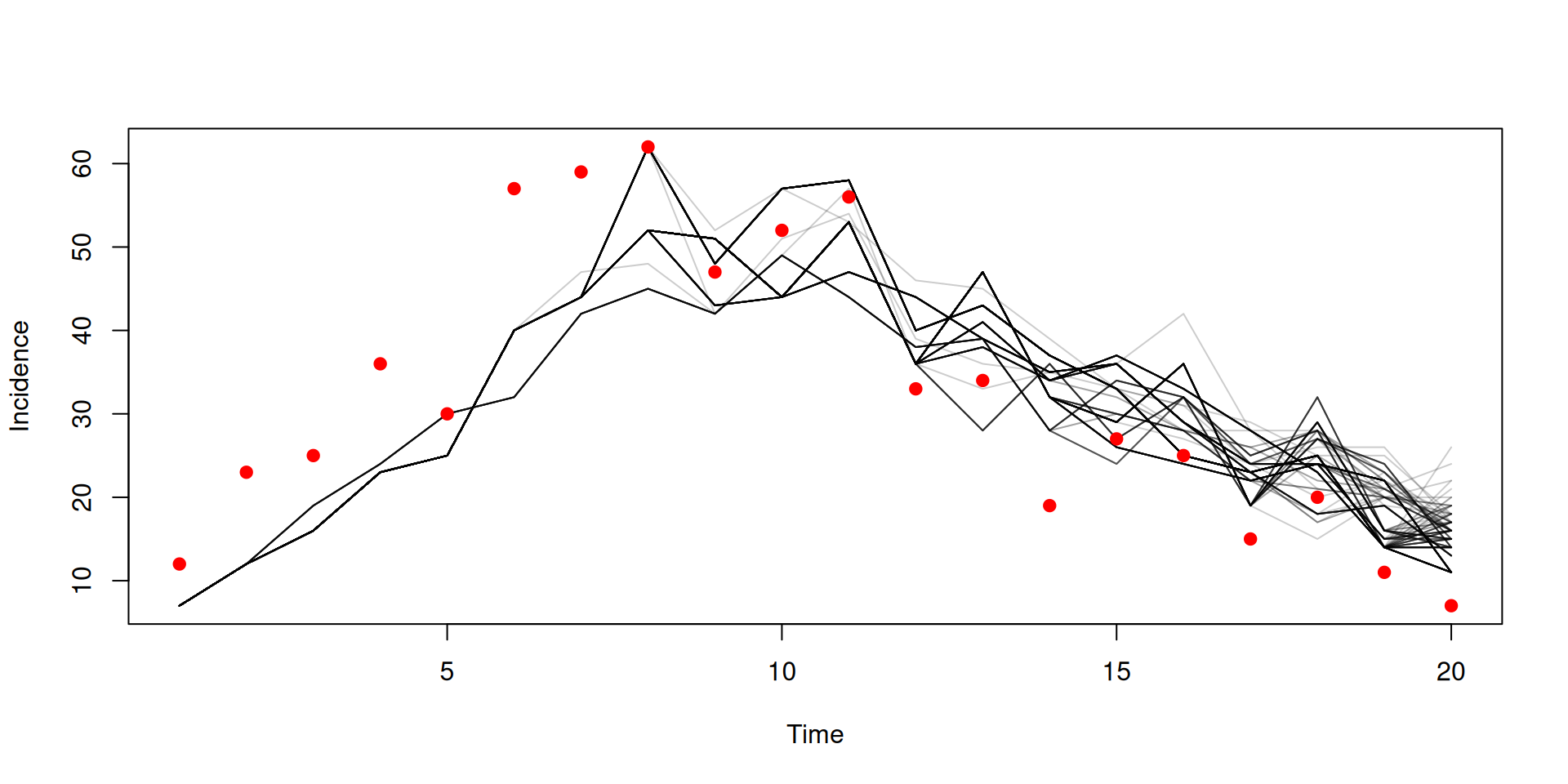
State space models
(aka, what is really going on here?)
What is it?
- A state space model (SSM) is a mathematical framework for modelling a dynamical system.
- It is built around two processes:
- state equations that describes the evolution of some latent variables (also referred as “hidden” states) over time
- observation equations that relates the observations to the latent variables.
Can you be more precise?
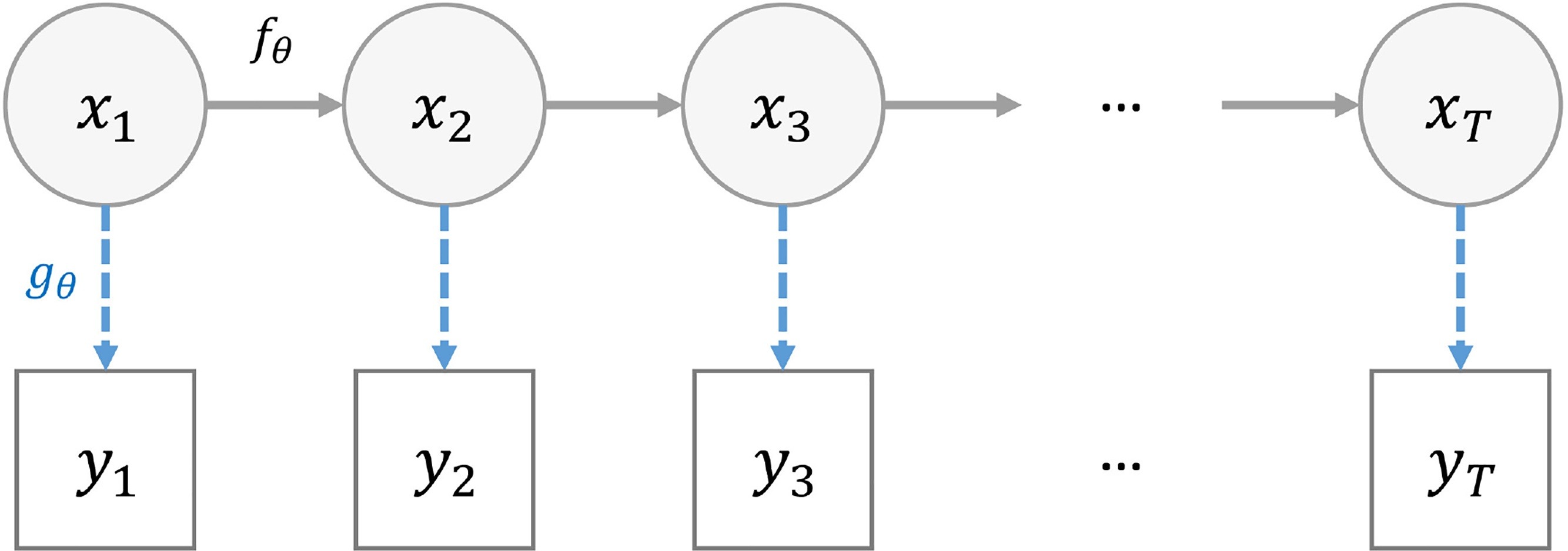
- \(x_{t, 1 \leq t \leq T}\) the hidden states of the system
- \(y_{t, 1 \leq t \leq T}\) the observations
- \(f_{\theta}\) the state transition function
- \(g_{\theta}\) the observation function
- \(t\) is often time
- \(\theta\) defines the model
Two common problems

- Two common needs
- “Filtering” i.e. estimate the hidden states \(x_{t}\) from the observations \(y_t\)
- “Inference” i.e. estimate the \(\theta\)’s compatible with the observations \(y_{t}\)
(Bootstrap) Sequential Monte Carlo
AKA, the particle filter
Assuming a given \(\theta\), at each time step \(t\), BSSMC:
- generates \(X_{t+1}^N\) by using \(f_{\theta}(X_{t+1}^N|X_{t}^N)\) (the \(N\) particles)
- calculates weights for the newly generated states based on \(g_{\theta}(Y_{t+1}|X_{t+1})\)
- resamples the states to keep only the good ones
Allow to explores efficiently the state space by progressively integrating the data points
Produces a MC approximation of \(p(Y_{1:T}|\theta)\) the marginal likelihood
The filter in action
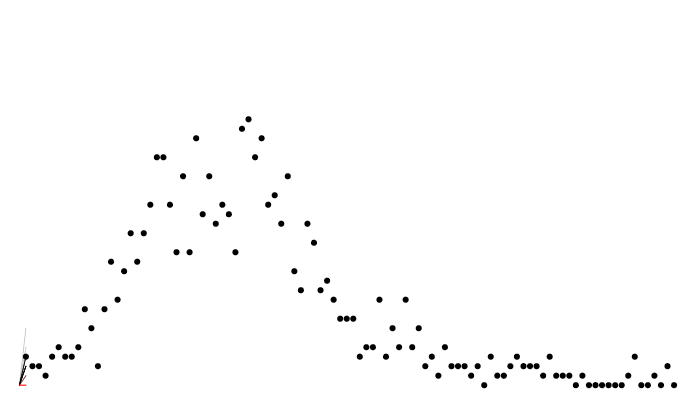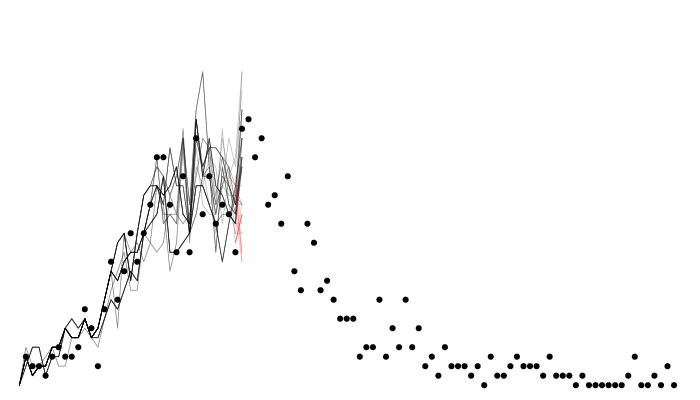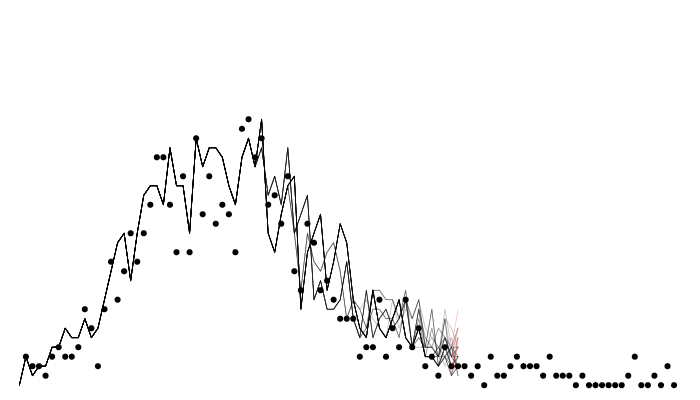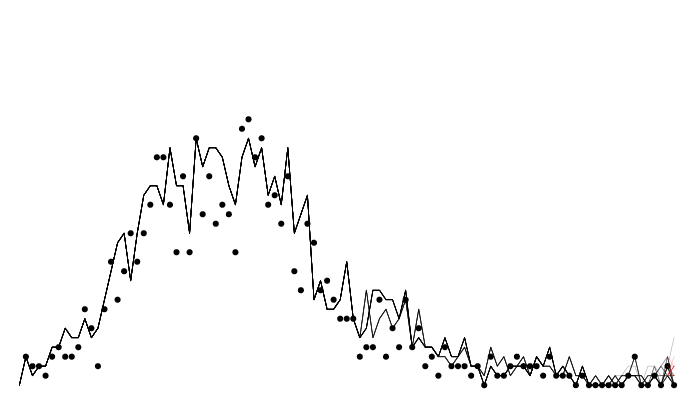
Particle MCMC
What is Particle MCMC?
- PMCMC is an algorithm which performs “filtering” and “inference”
- A Markov Chain Monte Carlo (MCMC) method for estimating target distributions
- MCMC explores the parameter space by moving randomly making jumps from one value to the next
- Probability of going from point to the other is determined by the proposal distribution and the ratio of the likelihood
- Compared with “traditional” MCMC, in PMCMC, the likelihood estimation is approximated using a “particle filter”
- The filter generates a set of “particles” i.e. trajectories compatible with the observation
- It uses these trajectories to compute a (marginal) likelihood that can be use by the PMCMC
Core algorithm
- Initialisation Start with a value \(\theta_{0}\) from the parameter space
- Initial SMC Use sequential Monte Carlo to do the “filtering” and samples of potential \(\{X_{t}\}_{1..N}\). Calculate the (marginal) likelihood from this using a MC estimator
- Proposal Propose a new parameter value \(\theta ^*\)
- SMC Calculate marginal likelihood of proposal
- Metropolis-Hastings Accept with probability \(\min(1, \alpha)\) with \(\alpha = \frac{p(\theta ^*)}{p(\theta_{t})} \cdot \frac{q(\theta_{t})}{q(\theta ^*)}\)
- Loop Redo (3) until the number of steps is reached
monty & dust2
dust2- implements bootstrap particle filter
- can run models in parallel
monty- implements MCMC with support for stochastic probability densities
- we are adding additional samplers (adaptive MCMC, HMC, but most can’t be used with stochastic densities)
mcstate- used to contain all of this (plus SMC^2, IF)
- Inference tooling for the Centre’s UK COVID model & other diseases
Design philosophy
- More complex structures are built up from simpler objects
- Filter {data, model, n_particles}
- PMCMC {parameters, filter}
- Provides you with low-level tools, and little hand-holding
- Pretty fast though
PMCMC
We have a marginal likelihood estimator from our particle filter:
How do we sample from beta and gamma?
We need:
- to tidy up our parameters
- to create a prior
- to create a posterior
- to create a sampler
“Parameters”
- Our filter takes a list of
betaandgamma,pars- it could take all sorts of other things, not all of which are to be estimated
- some of the inputs might be vectors or matrices
- Our MCMC takes an unstructured vector \(\theta\)
- we propose a new \(\theta^*\) via some kernel, say a multivariate normal requiring a matrix of parameters corresponding to \(\theta\)
- we need a prior over \(\theta\), but not necessarily every element of
pars
- Smoothing this over is a massive nuisance
- some way of mapping from \(\theta\) to
pars(and back again)
- some way of mapping from \(\theta\) to
Parameter packers
Our solution, “packers”
packer <- monty_packer(c("beta", "gamma"))
packer
#>
#> ── <monty_packer> ──────────────────────────────────────────────────────────────
#> ℹ Packing 2 parameters: 'beta' and 'gamma'
#> ℹ Use '$pack()' to convert from a list to a vector
#> ℹ Use '$unpack()' to convert from a vector to a list
#> ℹ See `?monty_packer()` for more informationWe can transform from \(\theta\) to a named list:
Parameter packers
Bind additional data
Parameter packers
Cope with vector-valued parameters in \(\theta\)
packer <- monty_packer(array = c(beta = 3, gamma = 3))
packer
#>
#> ── <monty_packer> ──────────────────────────────────────────────────────────────
#> ℹ Packing 6 parameters: 'beta[1]', 'beta[2]', 'beta[3]', 'gamma[1]', 'gamma[2]', and 'gamma[3]'
#> ℹ Use '$pack()' to convert from a list to a vector
#> ℹ Use '$unpack()' to convert from a vector to a list
#> ℹ See `?monty_packer()` for more information
packer$unpack(c(0.2, 0.21, 0.22, 0.1, 0.11, 0.12))
#> $beta
#> [1] 0.20 0.21 0.22
#>
#> $gamma
#> [1] 0.10 0.11 0.12Priors
Another DSL, similar to odin’s:
prior <- monty_dsl({
beta ~ Exponential(mean = 0.5)
gamma ~ Exponential(mean = 0.3)
})
prior
#>
#> ── <monty_model> ───────────────────────────────────────────────────────────────
#> ℹ Model has 2 parameters: 'beta' and 'gamma'
#> ℹ This model:
#> • can compute gradients
#> • can be directly sampled from
#> • accepts multiple parameters
#> ℹ See `?monty_model()` for more informationThis is a “monty model”
compute this density manually:
From a dust filters to a monty model
Combine a filter and a packer
packer <- monty_packer(c("beta", "gamma"))
likelihood <- dust_likelihood_monty(filter, packer)
likelihood
#>
#> ── <monty_model> ───────────────────────────────────────────────────────────────
#> ℹ Model has 2 parameters: 'beta' and 'gamma'
#> ℹ This model:
#> • is stochastic
#> ℹ See `?monty_model()` for more informationPosterior from likelihood and prior
Combine a likelihood and a prior to make a posterior
\[ \underbrace{\Pr(\theta | \mathrm{data})}_{\mathrm{posterior}} \propto \underbrace{\Pr(\mathrm{data} | \theta)}_\mathrm{likelihood} \times \underbrace{P(\theta)}_{\mathrm{prior}} \]
(remember that addition is multiplication on a log scale)
Create a sampler
A diagonal variance-covariance matrix (uncorrelated parameters)
Use this to create a “random walk” sampler:
Let’s sample!
samples <- monty_sample(posterior, sampler, 1000, n_chains = 3)
samples
#>
#> ── <monty_samples: 2 parameters x 1000 samples x 3 chains> ─────────────────────
#> ℹ Parameters: 'beta' and 'gamma'
#> ℹ Conversion to other types is possible:
#> → ! posterior::as_draws_array() [package installed, but not loaded]
#> → ! posterior::as_draws_df() [package installed, but not loaded]
#> → ! coda::as.mcmc.list() [package installed, but not loaded]
#> ℹ See `?monty_sample()` and `vignette("samples")` for more informationThe result: diagnostics
Diagnostics can be used from the posterior package
## Note: as_draws_df converts samples$pars, and drops anything else in samples
samples_df <- posterior::as_draws_df(samples)
posterior::summarise_draws(samples_df)
#> # A tibble: 2 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 beta 0.904 0.902 0.126 0.110 0.679 1.14 1.04 84.6 36.8
#> 2 gamma 0.796 0.765 0.203 0.147 0.480 1.17 1.03 87.5 34.1The results: parameters
You can use the posterior package in conjunction with bayesplot (and then also ggplot2)
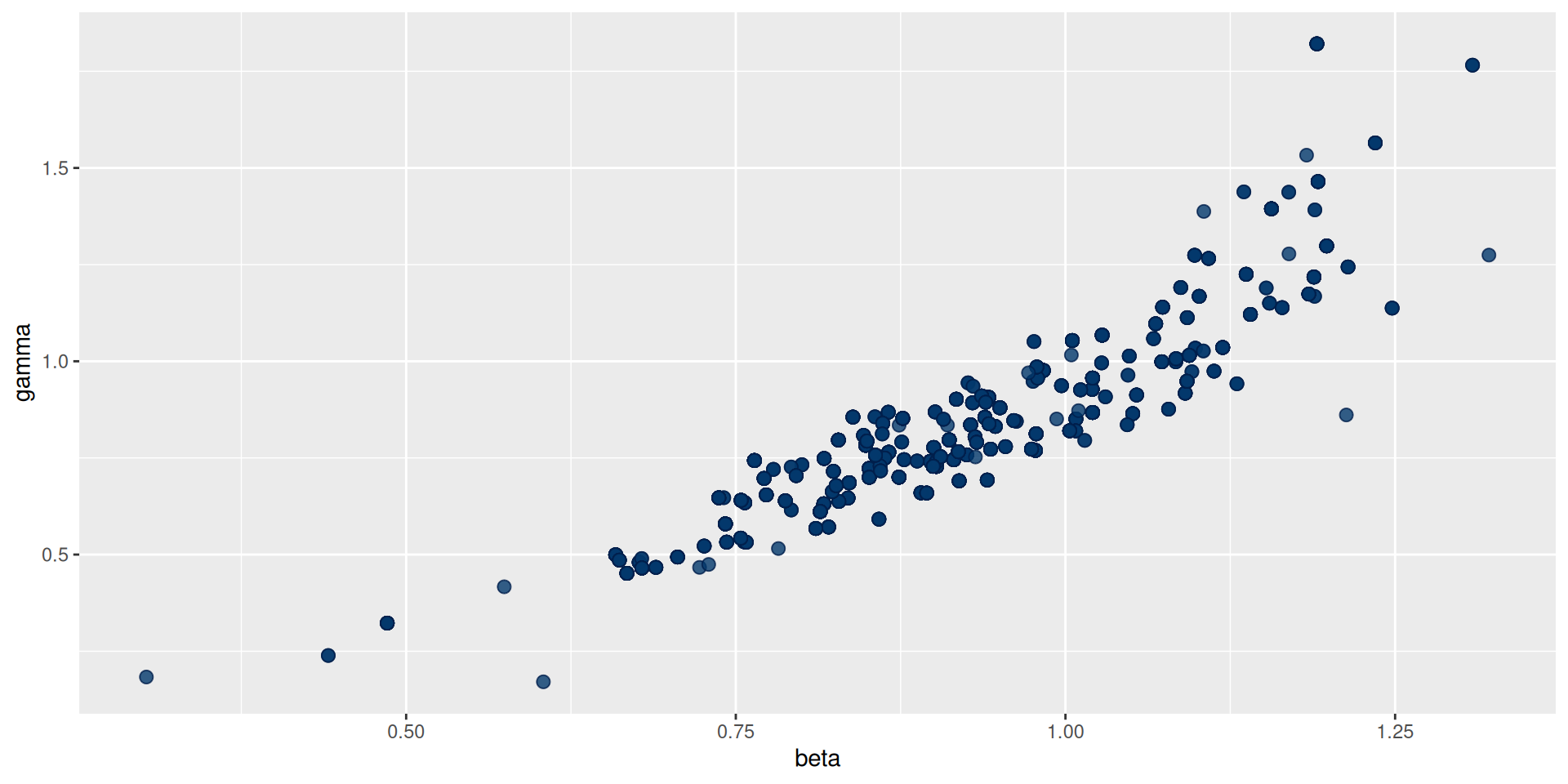
The result: traceplots
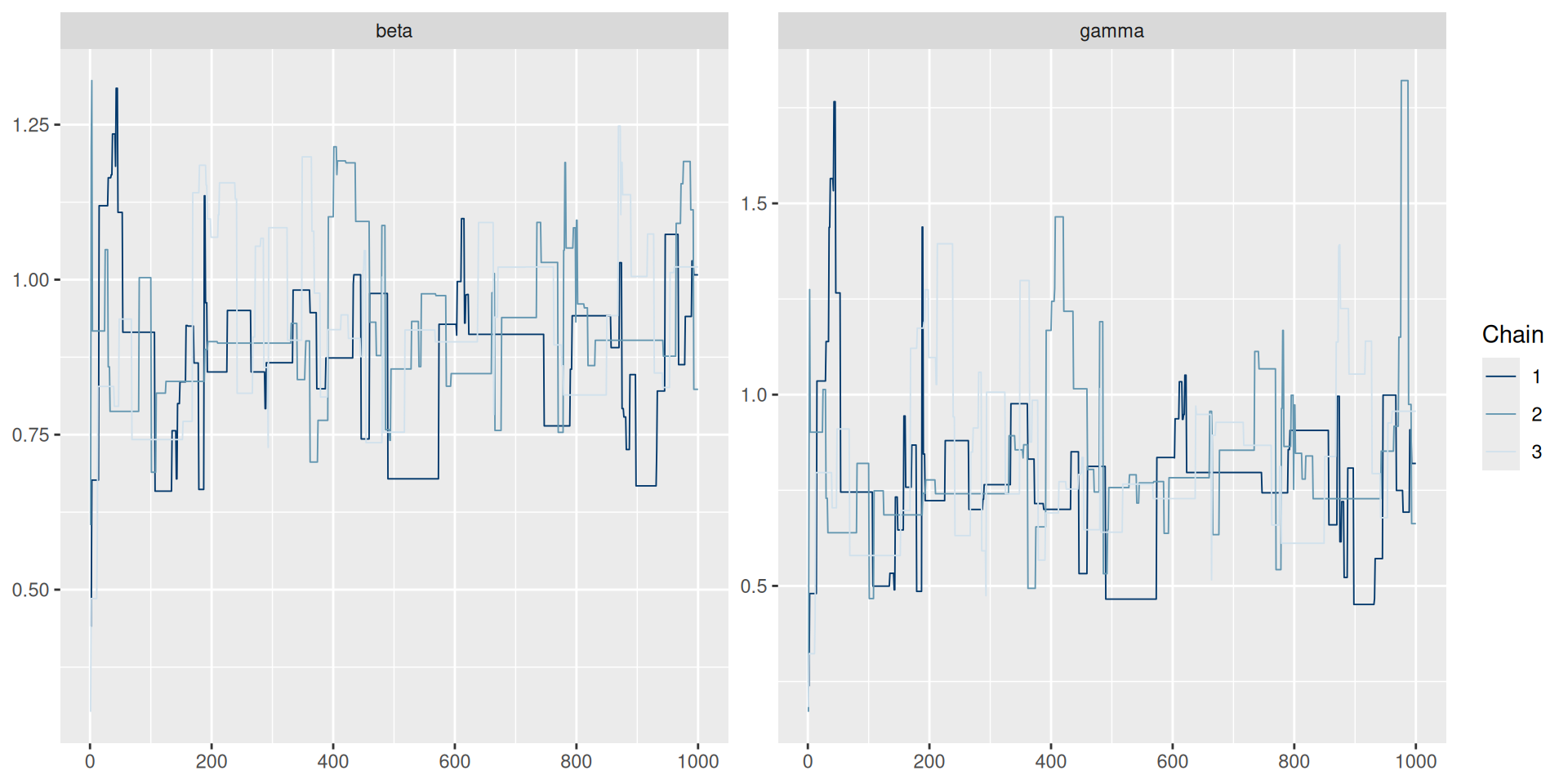
The result: density over time
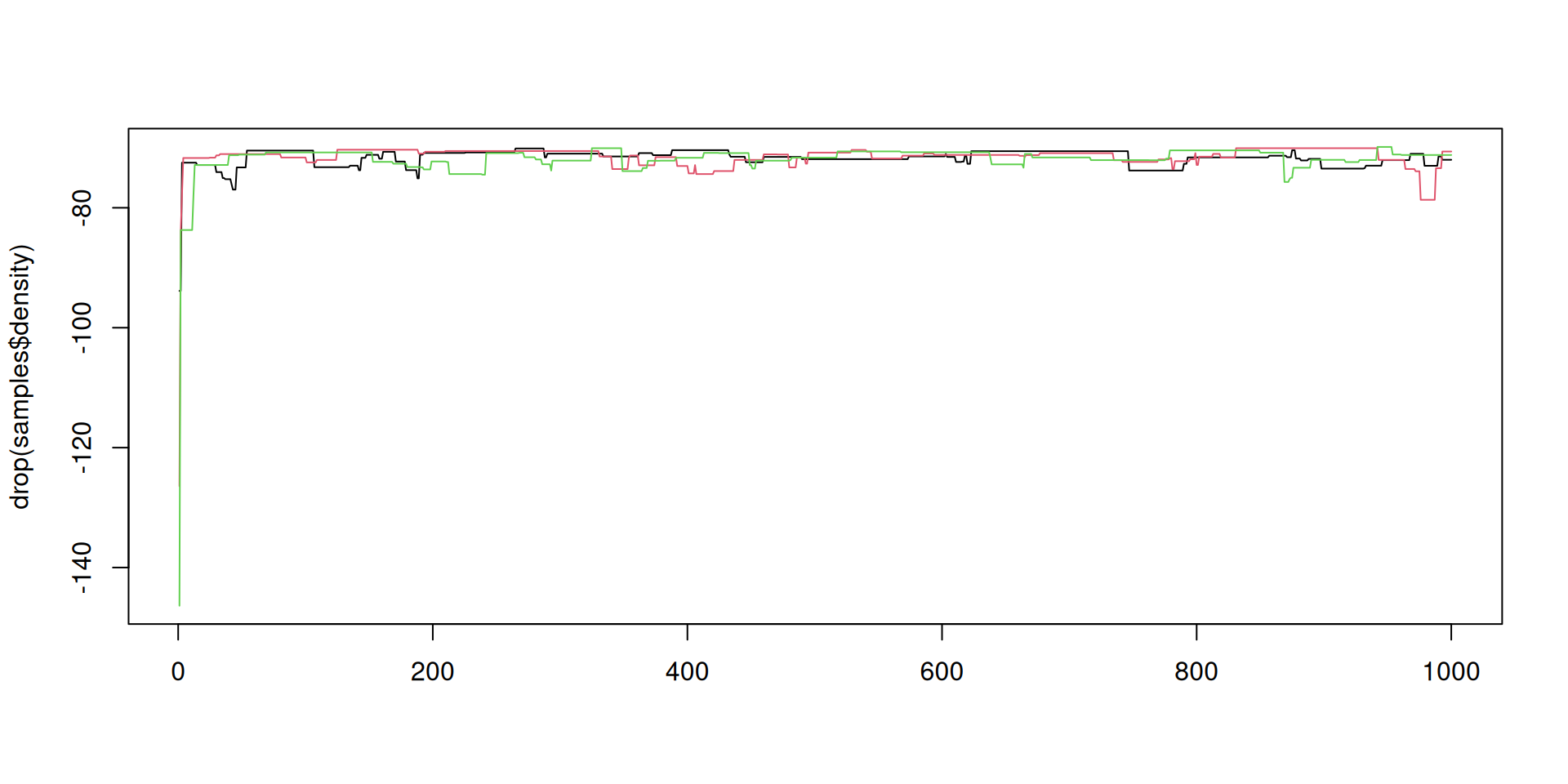
The result: density over time
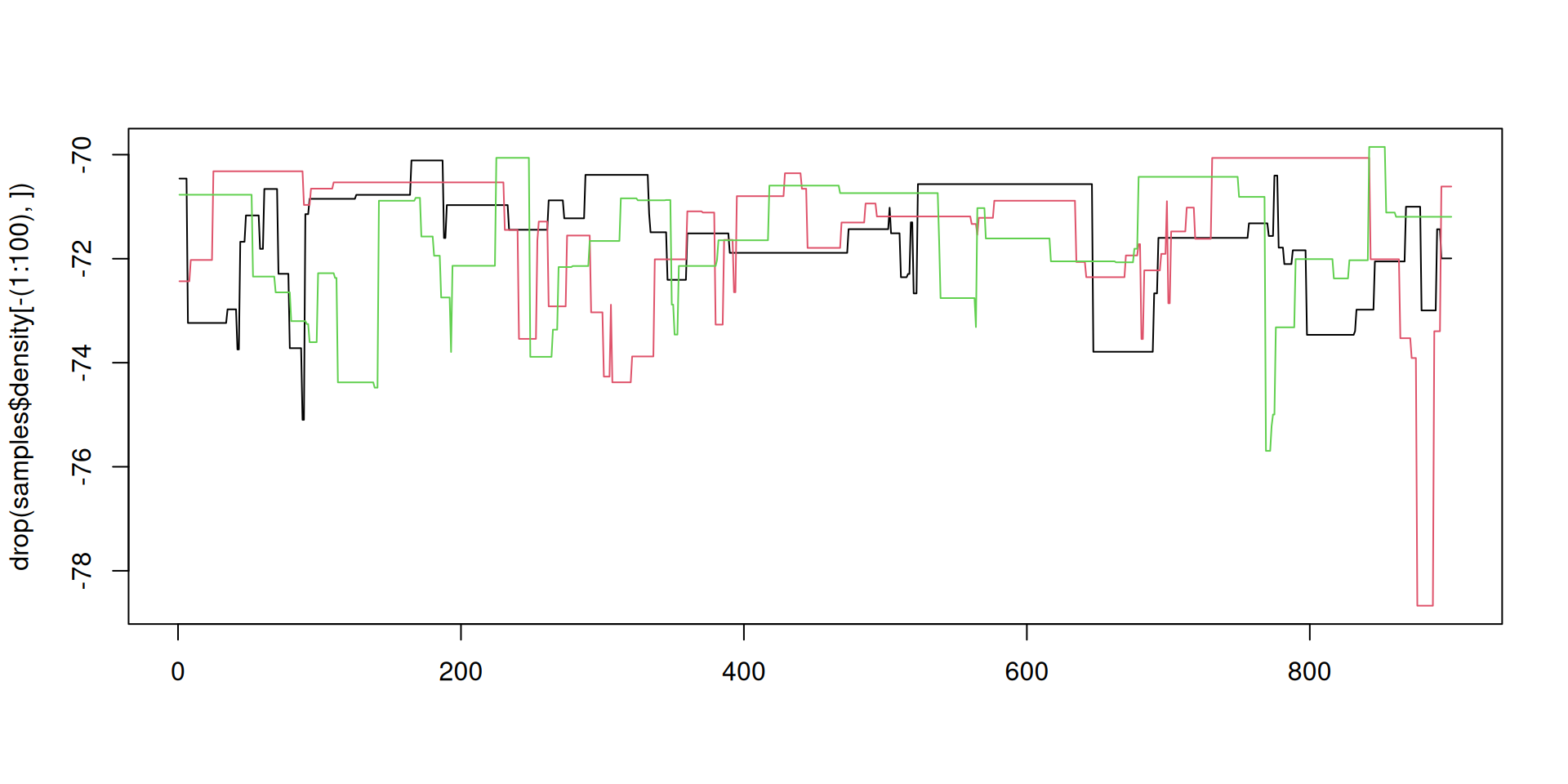
Better mixing
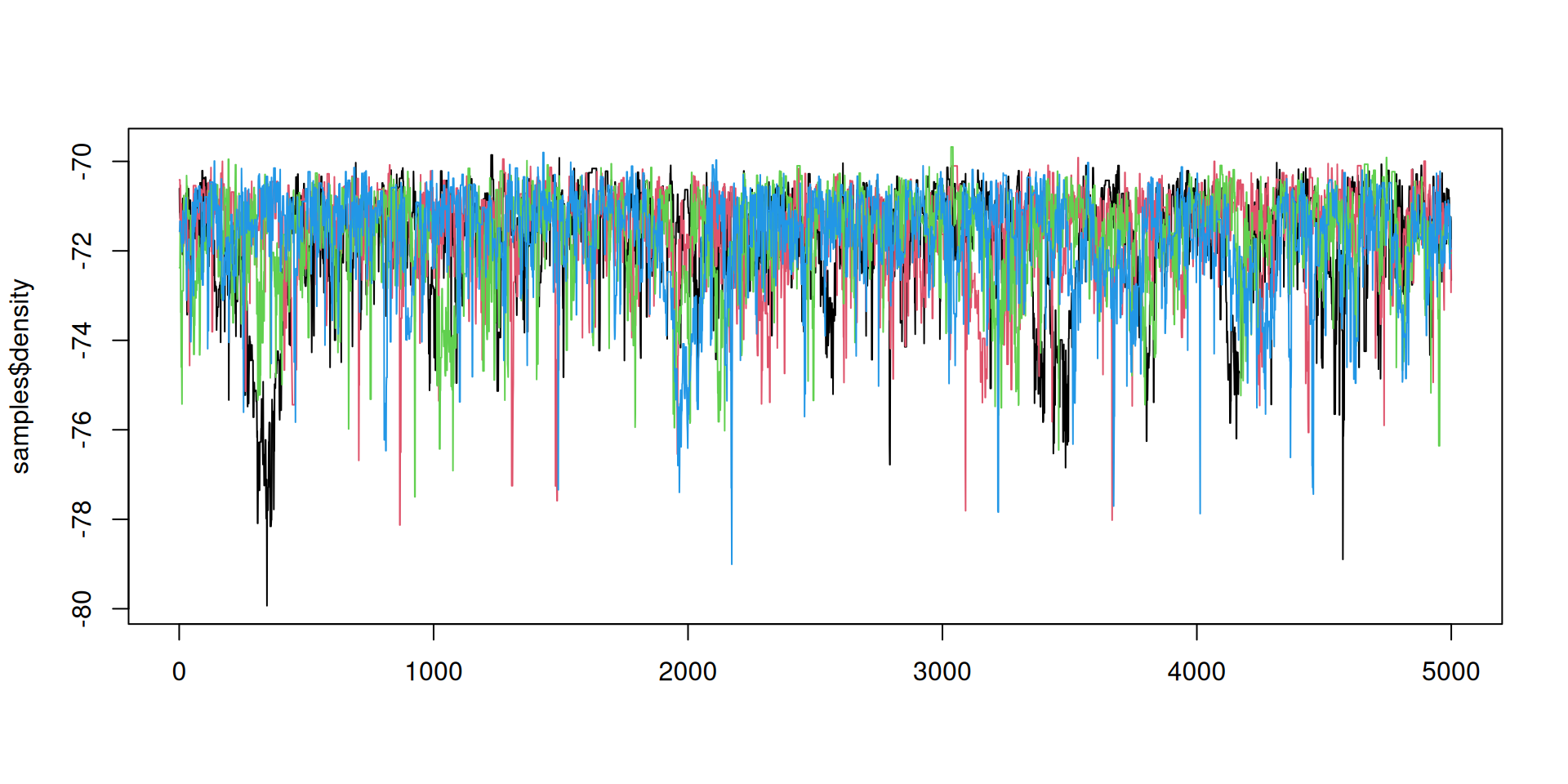
Better mixing: the results
samples_df <- posterior::as_draws_df(samples)
posterior::summarise_draws(samples_df)
#> # A tibble: 2 × 10
#> variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
#> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 beta 0.928 0.920 0.121 0.120 0.747 1.14 1.01 299. 404.
#> 2 gamma 0.834 0.801 0.202 0.185 0.567 1.21 1.02 239. 293.Better mixing: the results
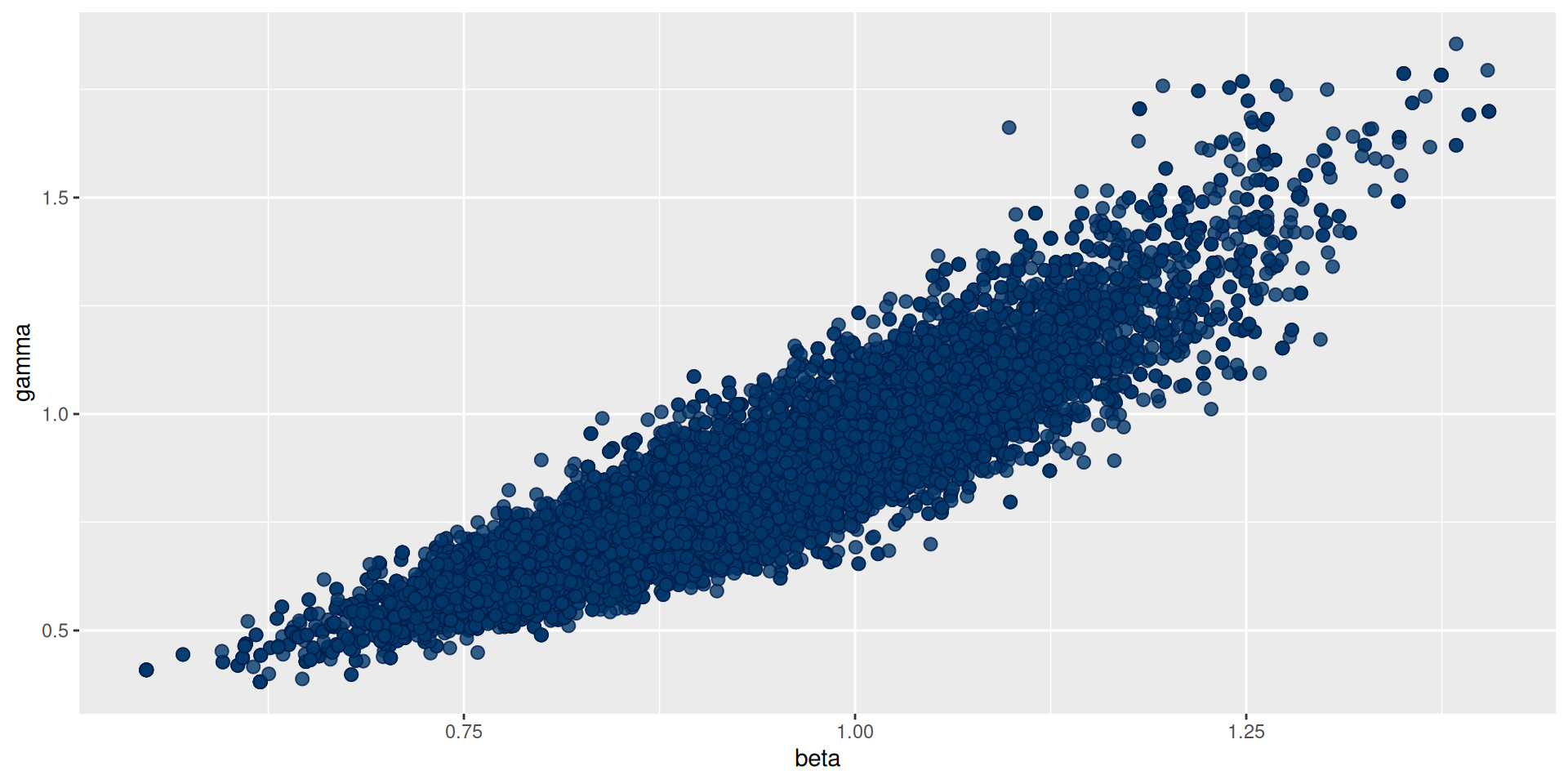
Better mixing: the results
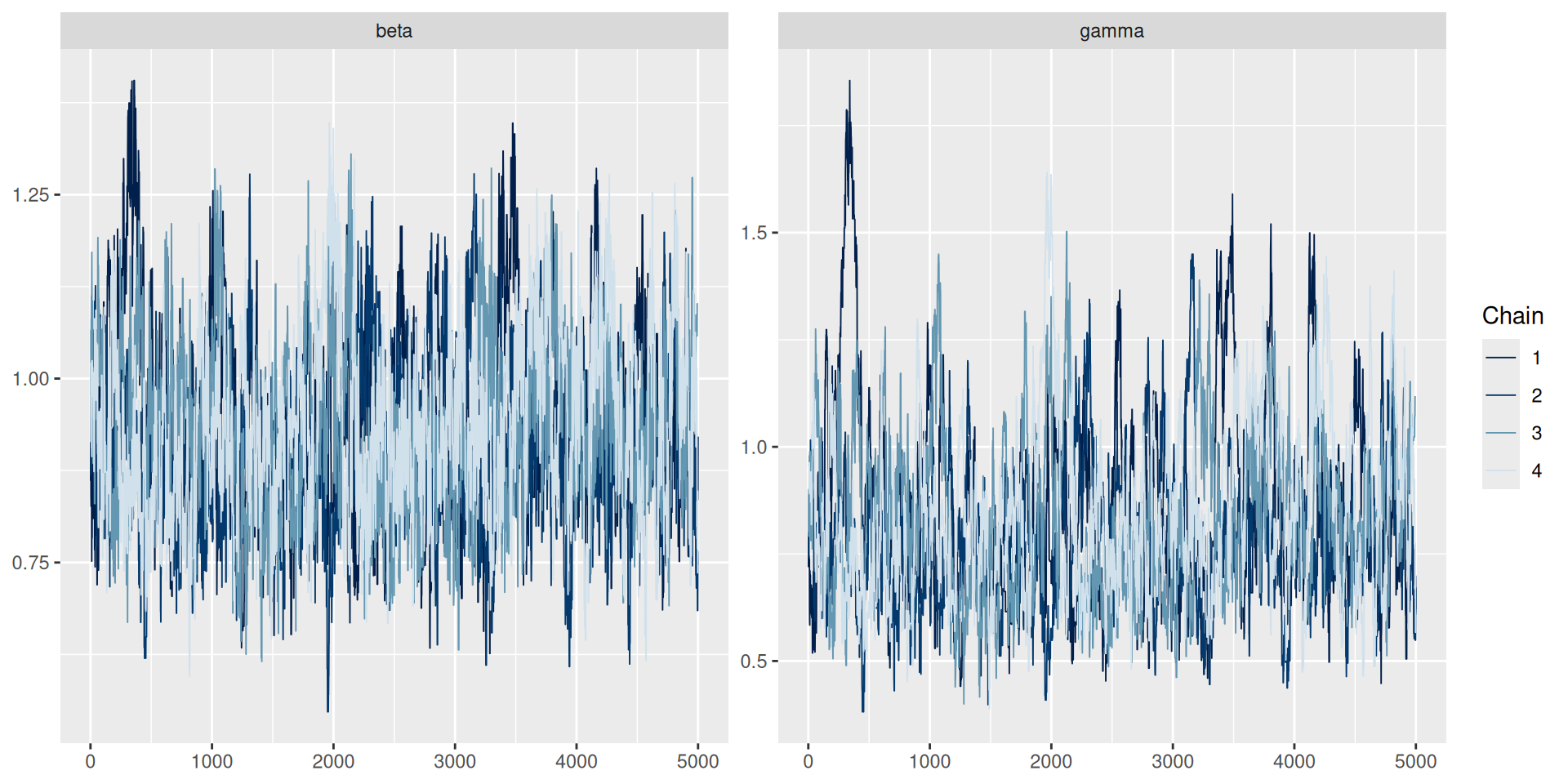
Parallelism
Two places to parallelise
- among particles in your filter
- between chains in the sample
e.g., 4 threads per filter x 2 workers = 8 total cores in use
Configure the filter
Use the n_threads argument, here for 4 threads
requires that you have OpenMP; this is very annoying on macOS
Configure a parallel runner
Use monty_runner_callr, here for 2 workers
Pass runner through to monty_sample:
(sorry, this is broken unless your model is in a package!)
Run chains on different cluster nodes
Then queue these up on a cluster, e.g., using hipercow:
And retrieve the result
(sorry, also broken unless your model is in a package!)
Autocorrelation
- Notion from time series, which translates for (P)MCMC in term of the steps of the chains
- Autocorrelation refers to the correlation between the values of a time series at different points in time. In MCMC, this means correlation between successive samples.
- In the context of MCMC, autocorrelation can most of the time be substituted instead of “bad mixing”
- A signature of random-walk MCMC
- Likely to bias estimate (wrong mean) and reduce variance compared with the true posterior distribution
- Linked with the notion of Effective Sample Size, roughly speaking ESS gives the equivalent in i.i.d. samples
Autocorrelation in practice FAQ
- Why is Autocorrelation a Problem? For optimal performance, we want the samples to be independent and identically distributed (i.i.d.) samples from the target distribution.
- How to Detect Autocorrelation? We can calculate the autocorrelation function (ACF), which measures the correlation between the samples and their lagged values.
- How to Reduce Autocorrelation? To mitigate the problem of autocorrelation, there’s a number of strategies, including: using a longer chain, adapting the proposal distribution, using thinning or subsampling techniques. By reducing autocorrelation, we can obtain better estimates of the target distribution and improve the accuracy of our Bayesian inference.
Thinning the chain
- Either before or after fit
- Faster and less memory to thin before
- More flexible to thin later
- No real difference if trajectories not saved
This is useful because most of your chain is not interesting due to the autocorrelation.
Thinning the chain
While running
After running
Saving history
- Save your trajectories at every collected sample
- Save the final state at every sample (for onward simulation)
Trajectories
Trajectories
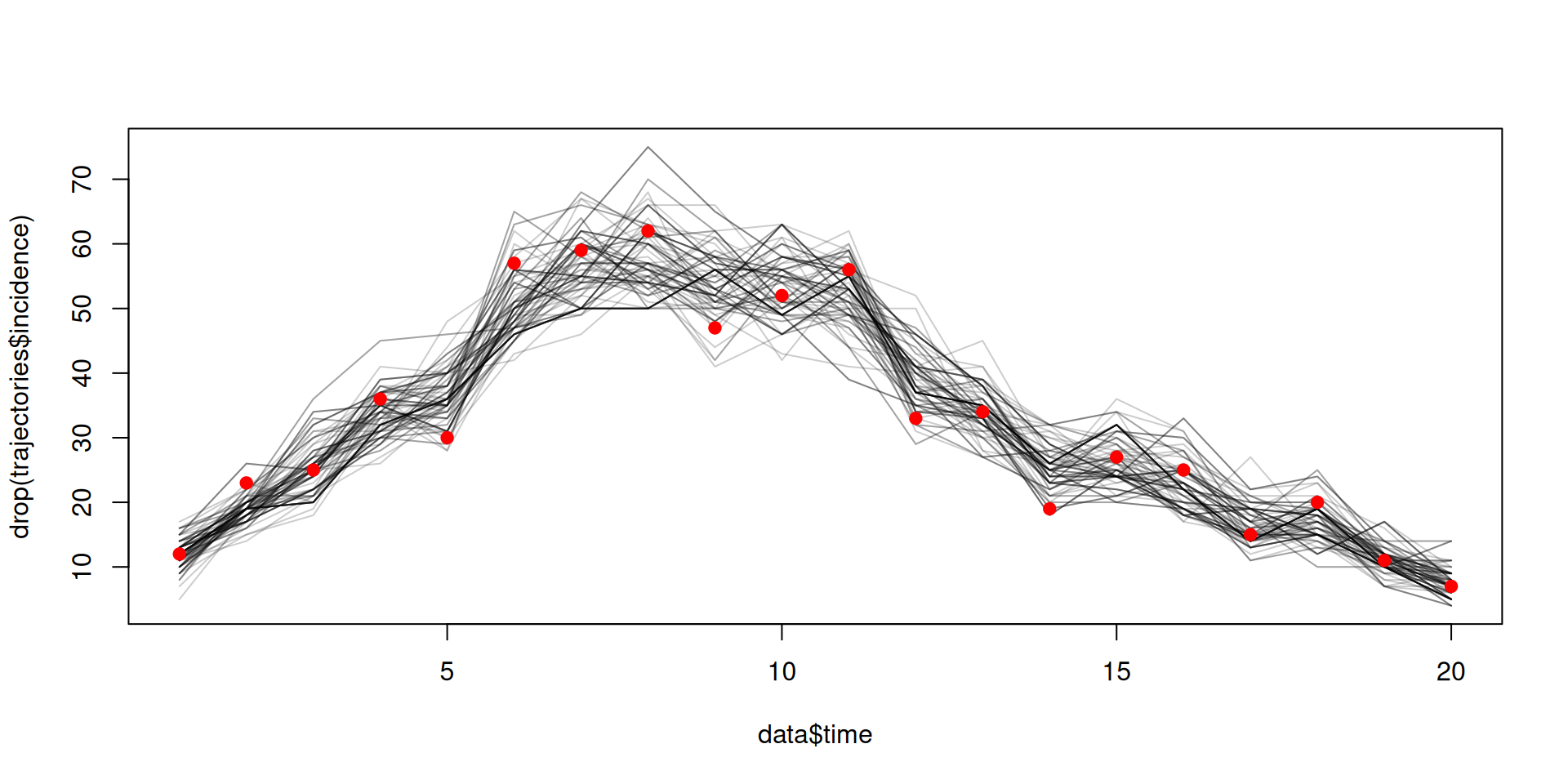
Next steps
- forward time predictions
- posterior predictive checks
- rerun filter in MCMC
- multi-parameter models
- deterministic (expectation) models as starting points
- adaptive fitting (deterministic models only)
- HMC
2025 Roadmap
- Some missing features from mcstate/dust1
- multi-stage filters
- restarting filters
- GPU-accelerated fitting
- SMC^2 and IF (perhaps)
- Some almost-ready features
- Parallel tempering (exploit parallelism, cope with multiple modes)
- Automatic differentiation
- NUTS and HMC algorithms