Malariaverse Workshop Bed nets

Pete Winskill

Session 3 💪!

Session aims:

Understand why bed nets can be challenging to model
Overview of bed net metrics and model inputs
Using 📦 [netz] to traverse the bed net landscape
Implementing bed nets in 📦 [malariasimulation]

Why can bed nets be tricky?

The effective coverage of bed nets today depends on the cumulative impacts of net distributions and net loss over many prior years.

Why can bed nets be tricky?

There are lots of bed net metrics:
- Delivery to country
- Distribution within country
- Crop (total number of nets within a country)
- Access and usage

Why can bed nets be tricky?

… and lots of other bed net variables to consider:
- Net type
- Net retention (or rate of loss)
- Distribution method/schedule (mass, routine etc.)
- Interaction with insecticide resistance
And finally, how we implement bed nets in 📦 [malariasimulation]

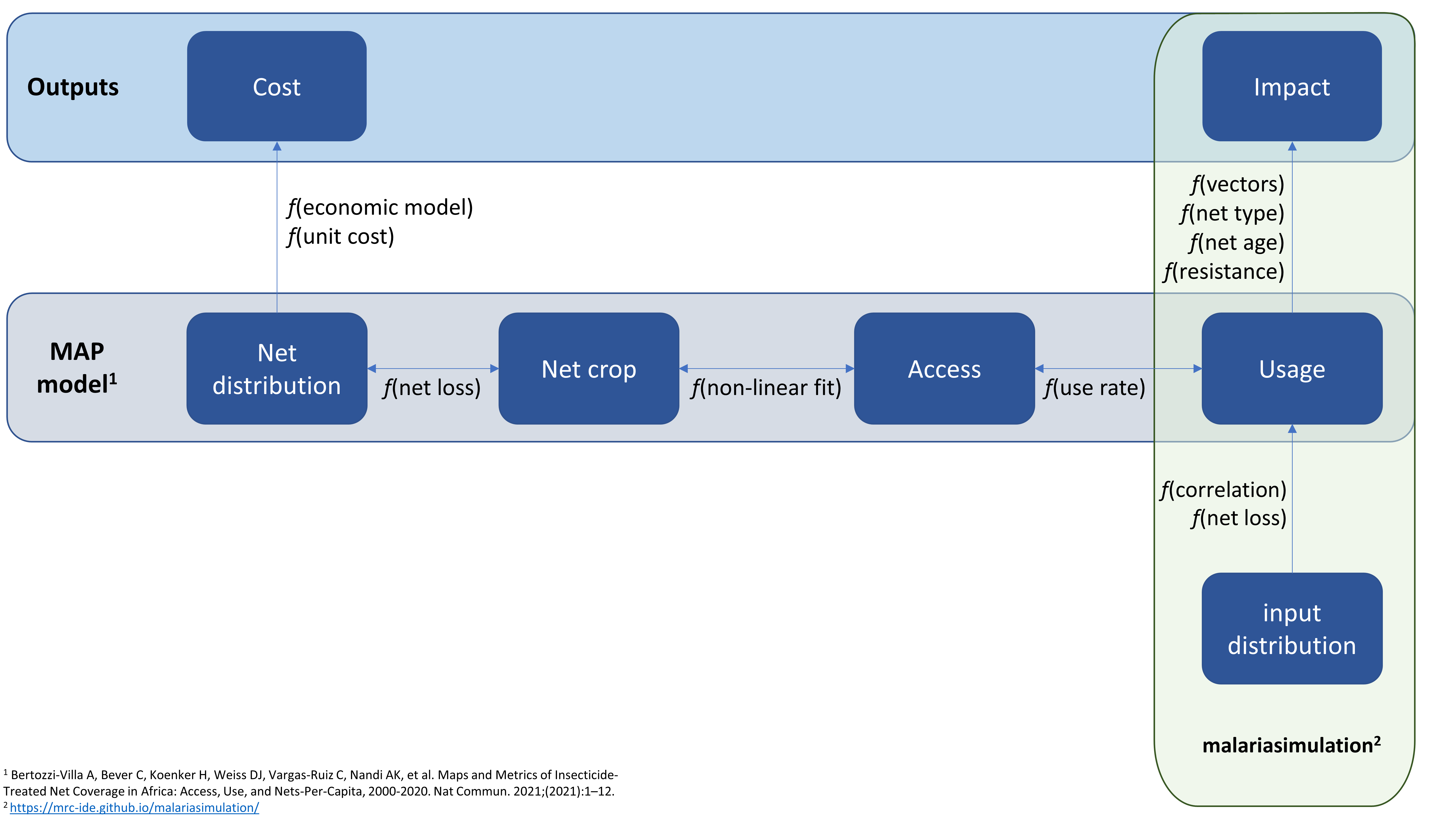
An empirical model of bed nets

Amelia Bertozzi-Villa et al have published a model linking bed net metrics for countries in SSA¹.
We can use this model to translate between the different bed net metrics
The model includes country-level fits

An empirical model of bed nets

The model triangulates net deliveries to a country with information on distributions and survey data on access and usage.

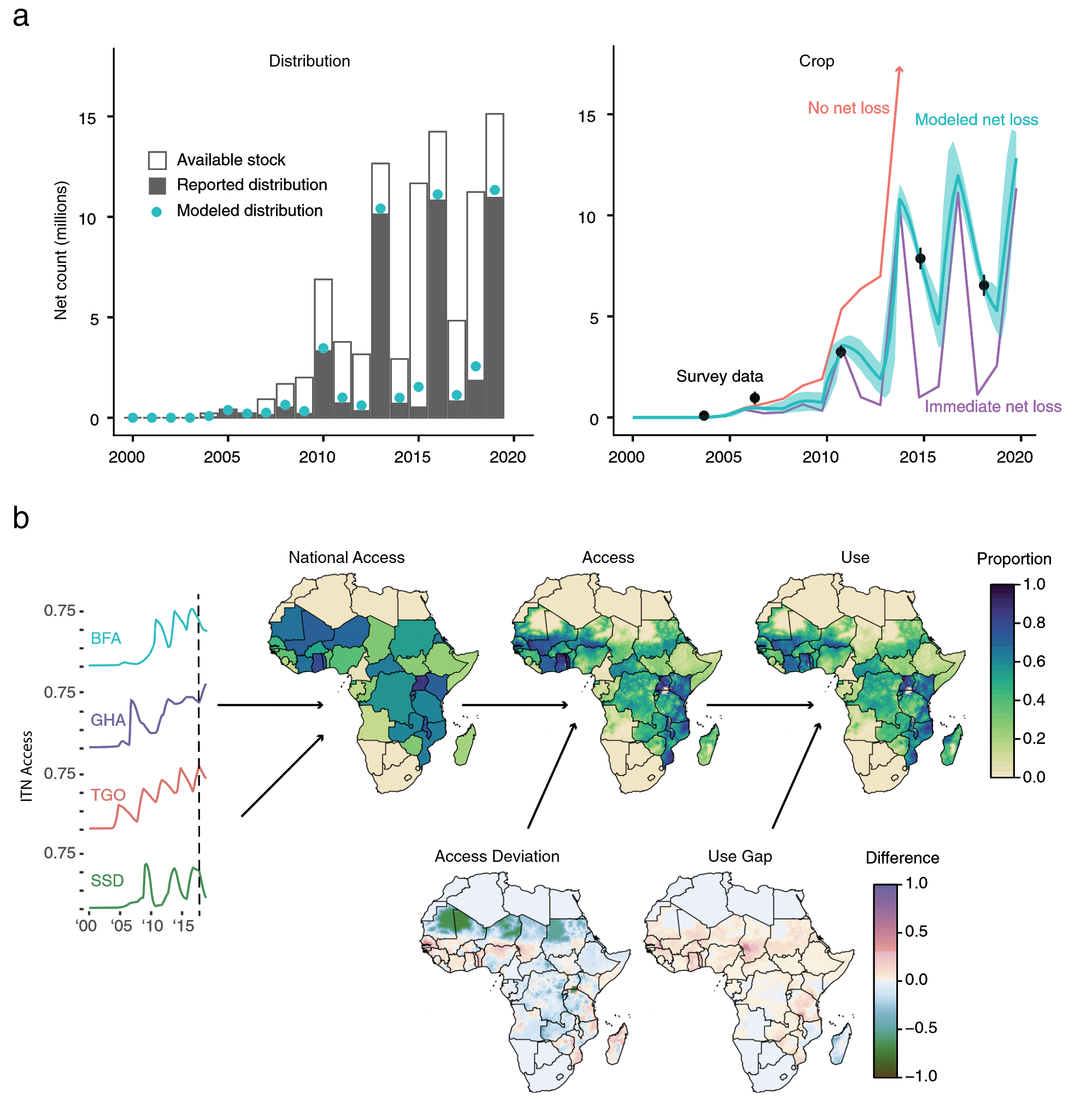
An empirical model of bed nets

The model also estimates country-specific net retention times

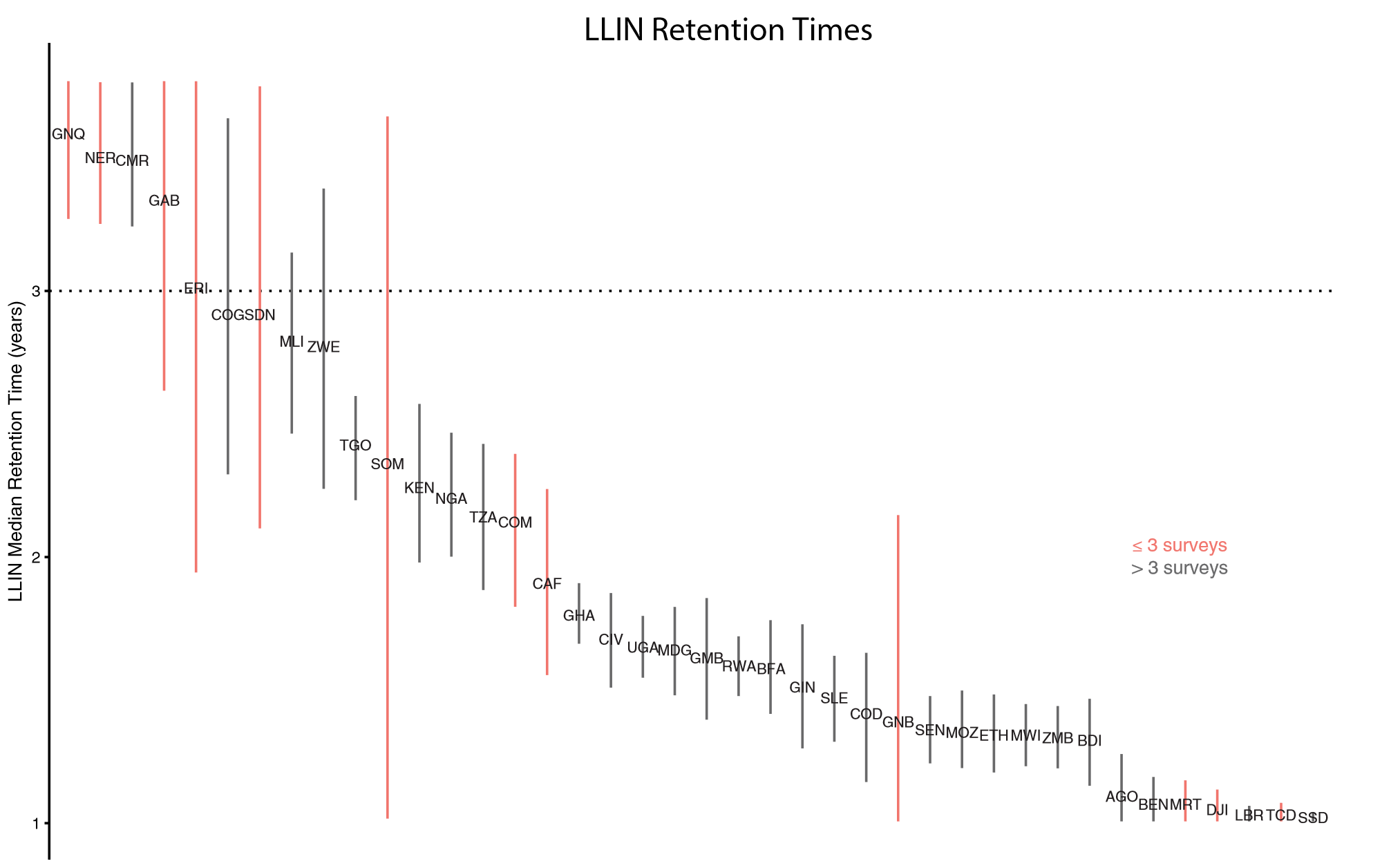
An empirical model of bed nets

Bertozzi-Villa et al show that access and crop are not linearly related (at the country level).
This can have big implications when costing a bet net campaign.

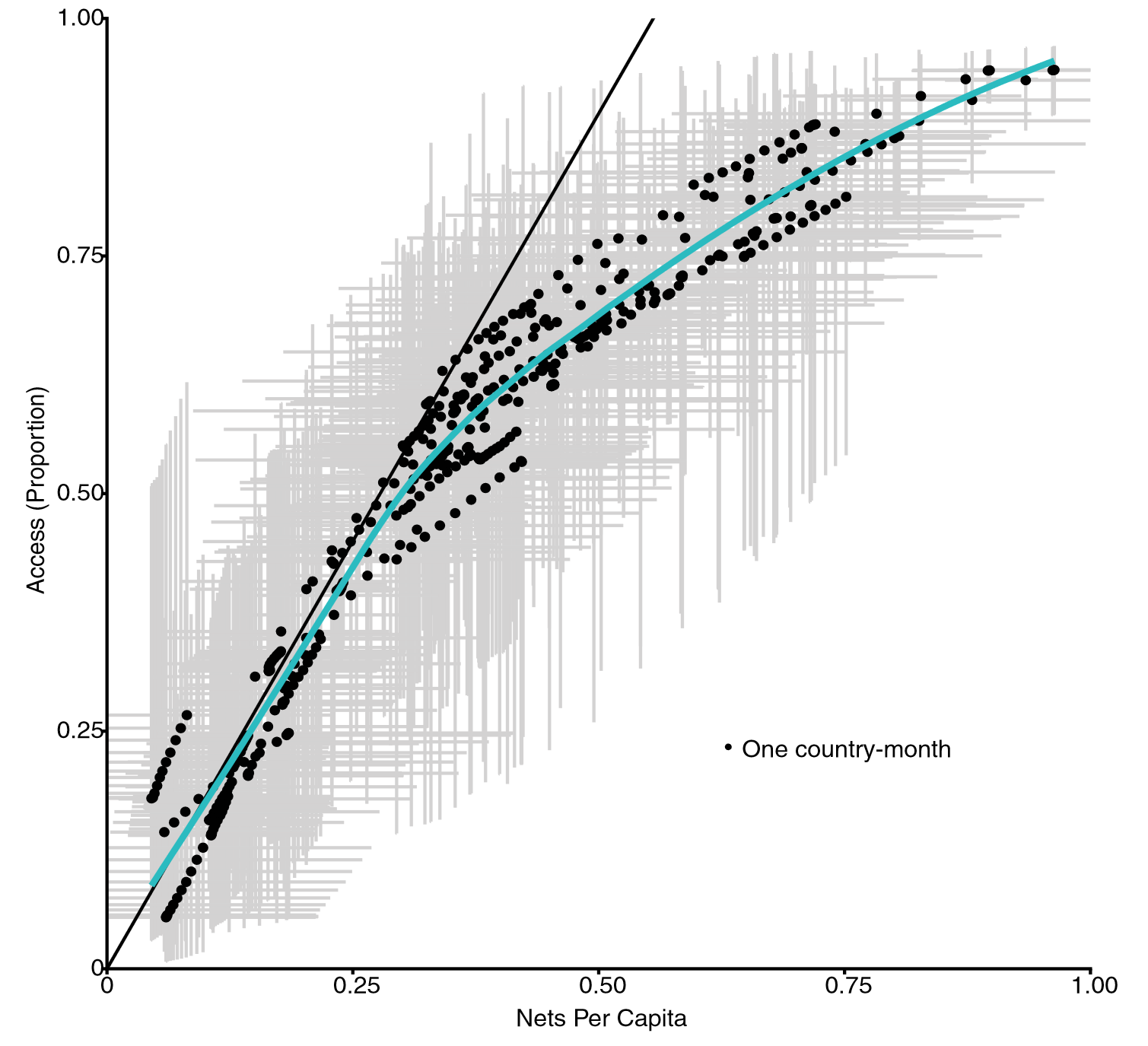
📦 [netz]

The 📦 [netz] has translated some of the work by Bertozzi-Villa et al.
It can facilitate translation between different bed net metrics.
It can be used to access country-specific data.
It also has functionality for specifying bed nets in 📦 [malariasimulation]

🙏 Big thank you to Nora for lots of hard work on 📦 [netz]!

Translating between bed net metrics with 📦 [netz]

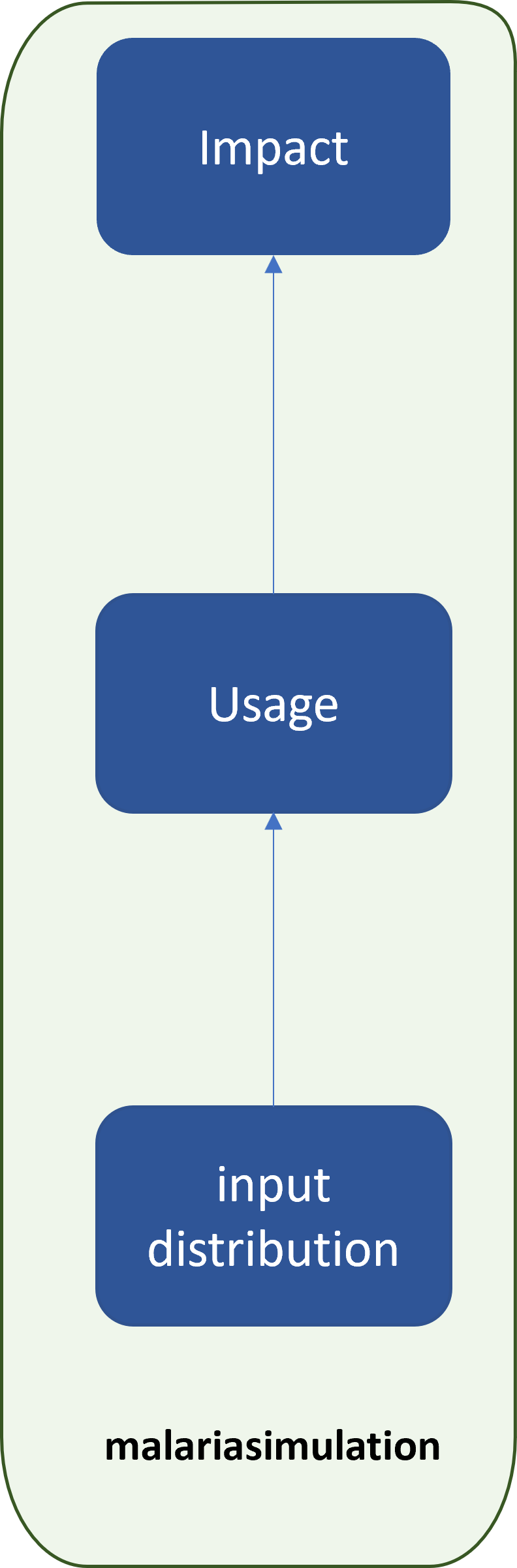
Schematic overview

Usage and Access

Usage: the proportion of people who have slept under a bed net the previous night. This is effective coverage.
Access: the proportion of the population that could sleep under a net.
📦 [netz] has functions to convert between usage and access:
- netz::usage_to_access(usage = 0.5, use_rate = 0.8)
- netz::access_to_usage(access = 0.5, use_rate = 0.8)
You can view empirical estimates of country use rates with:
- netz::get_usage_rate_data()

Access and crop

Access: the proportion of the population that could sleep under a net.
Crop: the total number of nets in the population. Crop increases with net distributions and decreases as nets are worn out and thrown away over time.
📦 [netz] has functions to convert between access and crop:
- netz::access_to_crop(access = 0.5)
- netz::crop_to_access(crop = 0.5)

Crop and distributions

Crop: the total number of nets in the population. Crop increases with net distributions and decreases as nets are worn out and thrown away over time.
Distribution: Nets distributed. These may be via mass-distributions or continuous distribution routes.
📦 [netz] has functions to convert between crop and distribution:
- netz::crop_to_distribution(crop = 0.5, distribution_frequency = 3 * 365, half_life = 2 * 365)
- netz::distribution_to_crop(crop = 0.5, distribution_frequency = 3 * 365, half_life = 2 * 365)
Net retention half-lives are estimated in the model by Bertozzi-Villa et al and can be accessed with:
- netz::get_halflife_data()

Crop and distributions

As crop is the cumulative impact of past distributions, different combinations of past distributions may lead to similar crop estimates. We can dynamically translate between no-equilibrium crop and distributions with:
- netz::crop_to_distribution_dynamic(crop = c(0.1, 0.2, 0.5, 0.1), netz::net_loss_map)
- netz::distribution_to_crop_dynamic(distribution = c(0.1, 0.2, 0.5, 0.1), netz::net_loss_map)

Net loss functions

Net retention can be modelled with different function forms.
In the model by Bertozzi-Villa et al, they use an s-shaped function form.
In 📦 [malariasimulation] net retention is exponentially distributed.
These are modelled by:
- netz::net_loss_map() and netz::net_loss_exp()
These functions can be passed when the argument net_loss_function is required.
We may to try and harmonise the bed net models at some point.

Bed nets in 📦 [malariasimulation]

Schematic overview

Implementing bed nets

In 📦 [malariasimulation] distributions in the model lead directly to effective coverage or usage.
We can use the 📦 [netz] population_usage() function to view the bed net usage in the model resulting from a given set of bed net distributions (model inputs):

netz::population_usage(
  timesteps = 365 * 30,
  distribution = rep(0.3, 10),
  distribution_timesteps = 365 * seq(1, 30, 3),
  half_life = 365 * 5
)

Implementing bed nets

Resulting population usage:

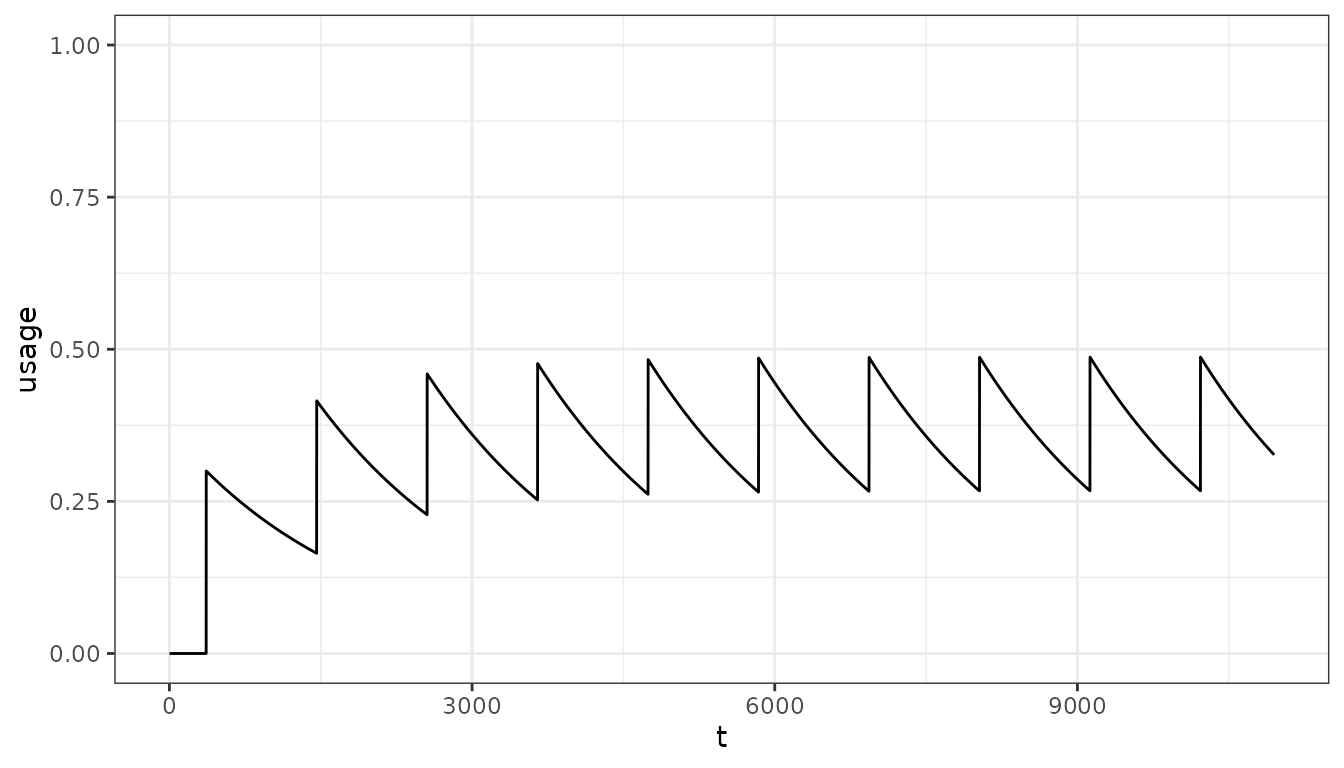
Implementing bed nets

More frequent distribution will lead to net usage to build to higher levels:

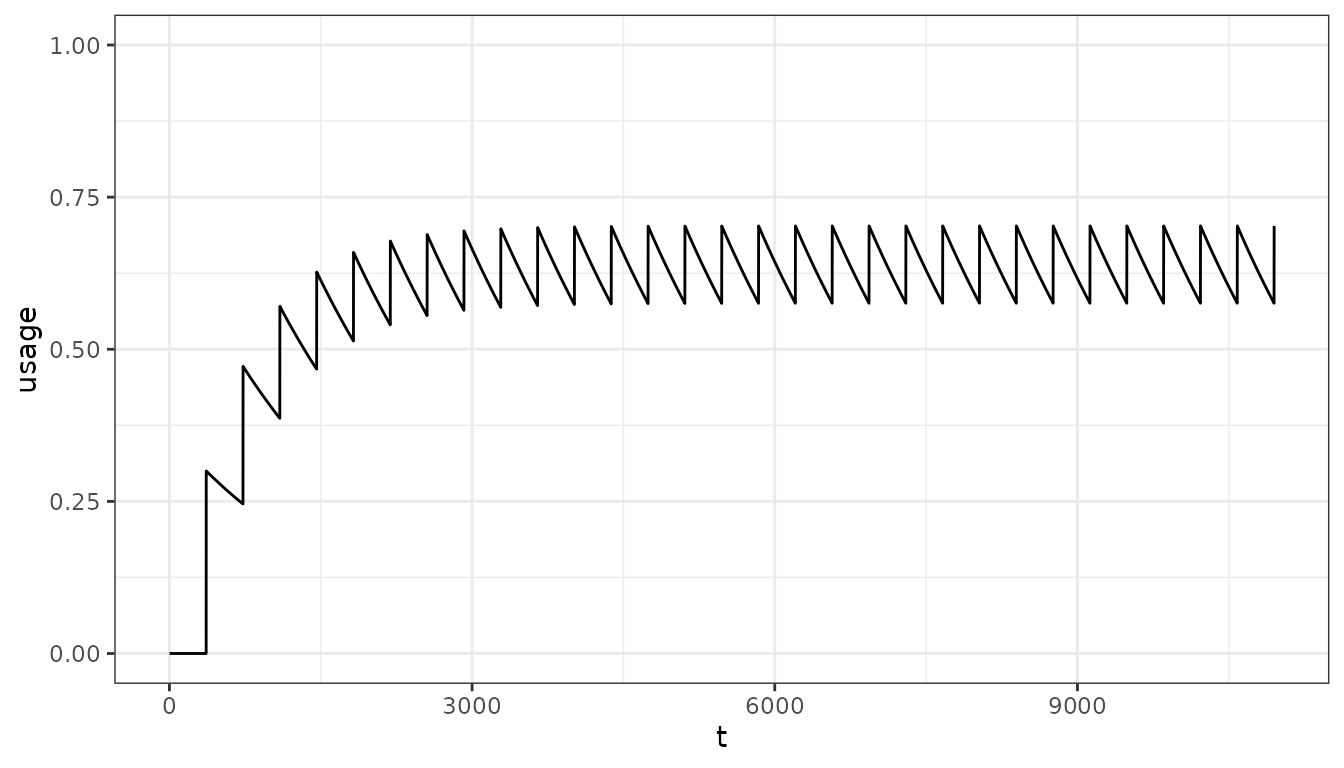
Implementing bed nets

As will larger distributions:

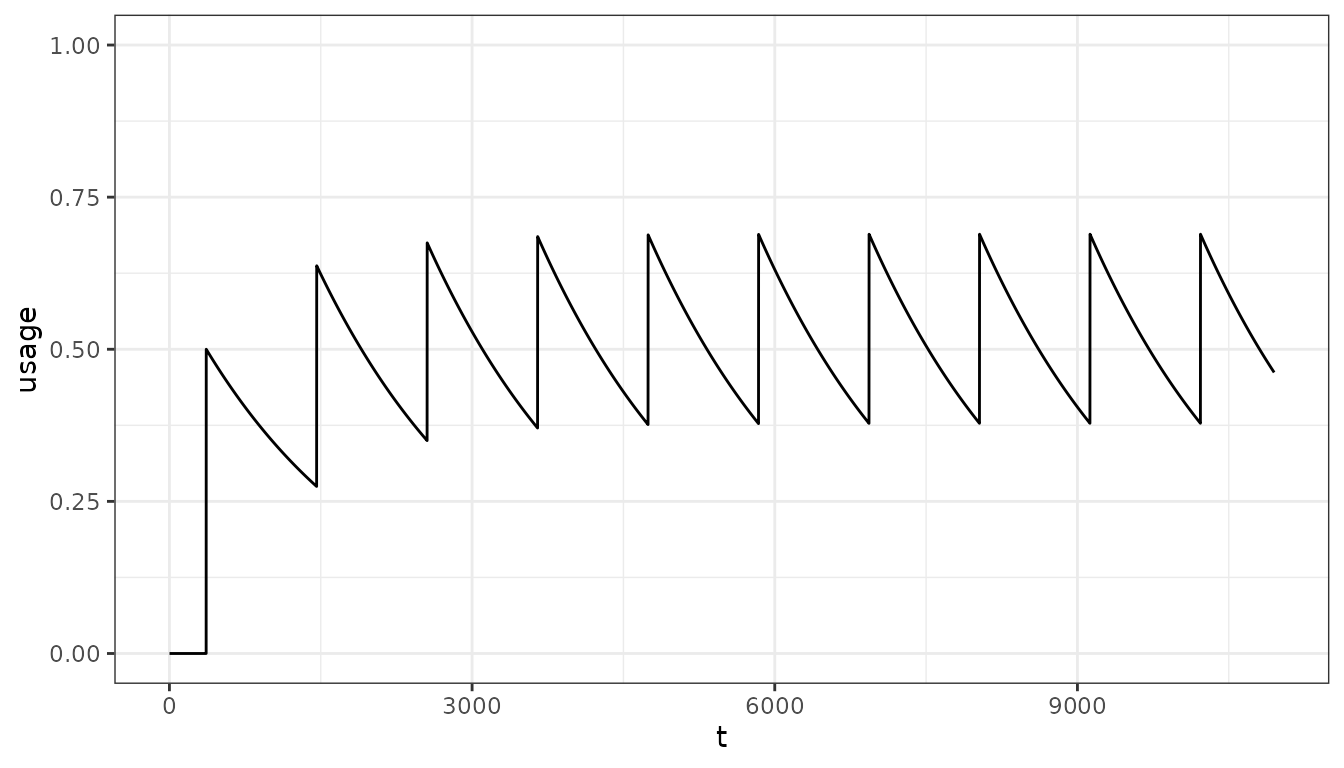
Implementing bed nets

We can also model irregular distributions:

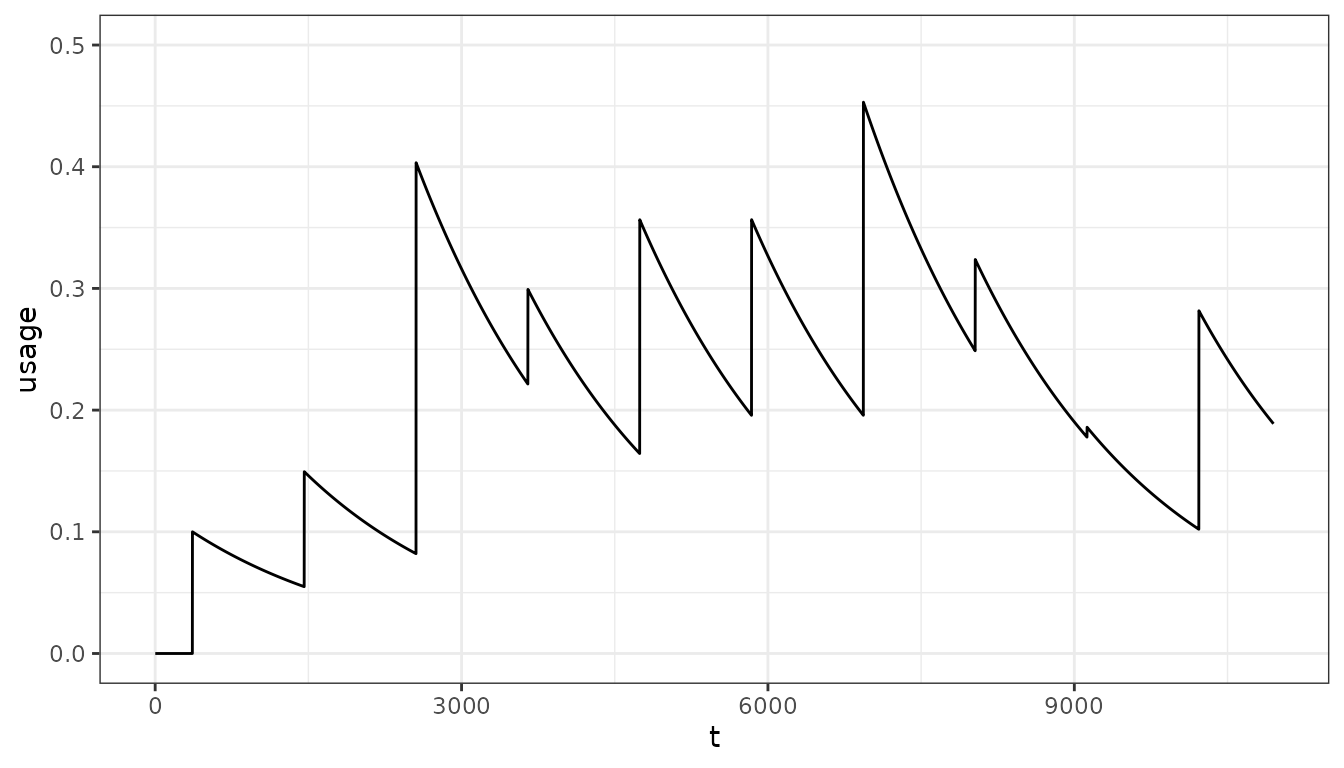
Fitting bed nets

In many cases we might have a set of observed population level usage estimates that we want to match to. We can use a non-linear optimiser to fit the distribution to these target usages:

# Target usage associated time points
target <- c(0.45, 0.33, 0.7)
target_tt <- c(2, 5, 9) * 365
# Time points at which distribution will occur
distribution_tt <- c(1, 4, 8) * 365

# Fit
fit <- netz::fit_usage(
  target_usage = target,
  target_usage_timesteps = target_tt,
  distribution_timesteps = distribution_tt
)

Fitting bed nets

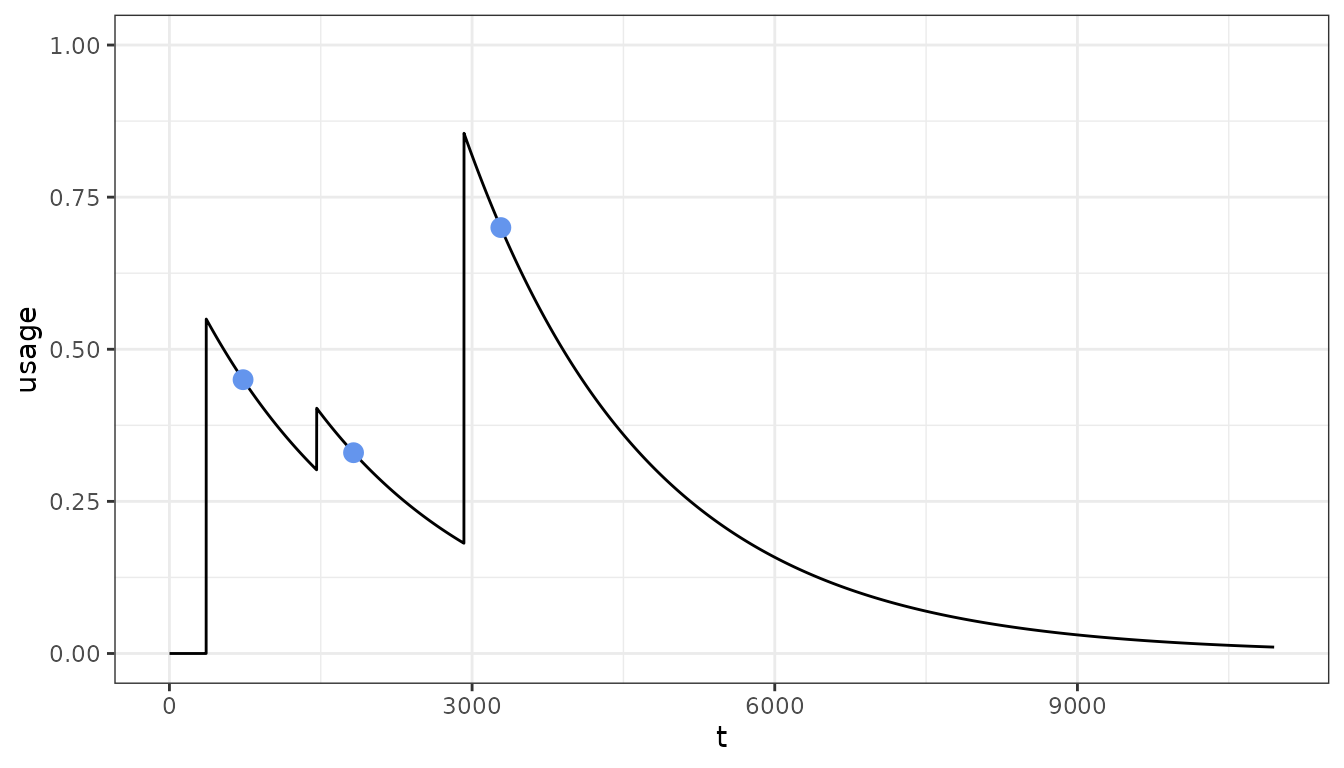
😵 Conversion overload! 😵

Bed nets in site files

We can look at the bed net inputs in the $interventions section of a site file.
You can see that as well as usage, we have the model input, net type, level of insecticide resistance and associated net efficacy parameters.

head(
  foresite::TGO$interventions[, c("iso3c", "name_1", "urban_rural", "year",
                                "itn_use", "itn_input_dist", "net_type",
                                "pyrethroid_resistance",
                                "dn0", "rn0", "rnm", "gamman")]
  )

  iso3c name_1 urban_rural year    itn_use itn_input_dist        net_type
1   TGO Centre       rural 2000 0.04239319   3.972372e-02 pyrethroid_only
2   TGO Centre       rural 2001 0.03059912   1.999607e-03 pyrethroid_only
3   TGO Centre       rural 2002 0.02194407   1.225237e-05 pyrethroid_only
4   TGO Centre       rural 2003 0.02110716   3.579113e-03 pyrethroid_only
5   TGO Centre       rural 2004 0.14395837   1.402791e-01 pyrethroid_only
6   TGO Centre       rural 2005 0.20412837   9.050257e-02 pyrethroid_only
  pyrethroid_resistance       dn0       rn0  rnm   gamman
1                  0.46 0.2933696 0.6736694 0.24 2.346871
2                  0.48 0.2899376 0.6761727 0.24 2.331779
3                  0.50 0.2869886 0.6783065 0.24 2.317303
4                  0.53 0.2826286 0.6814312 0.24 2.294338
5                  0.55 0.2792447 0.6838313 0.24 2.278917
6                  0.57 0.2763609 0.6858590 0.24 2.262831

Bed nets in site files

All of these bed net elements get translated into 📦 [malariasimulation] parameters when using the 📦 [site] site_parameters() function.
We also include future resistance extrapolations in the $resistance part of the site file.

🙏 No time today to explore all of the amazing work on insecticide resistance and net efficacy, but huge thanks to Tom, Ellie and others for all the hard work!

Let’s give it a try!

Run mvw::run_tutorial("Bednet")